摘要

近年来，材料基因组工程以及多尺度材料设计理论和计算方法的发展，为新型钴基高温合金的研发提供了新的思路。本文基于国内外新型钴基高温合金多尺度设计方面的成果以及本研究室多年来在该领域的研究工作，系统总结了材料多尺度计算方法在新型钴基高温合金领域的研究现状，总结了包括第一性原理、CALPHAD、相场法和机器学习方法在合金成分筛选、工艺设计和组织优化领域的多尺度耦合设计。在此基础上，针对各个研究方法的优势，展望了多尺度材料设计在新型钴基高温合金领域的发展趋势。

关键词： 高温合金 ; 多尺度设计 ; 计算材料学 ; 材料基因

高温合金是航空航天领域的关键材料，新型高温合金的研发和航空工业的发展息息相关[1]。目前，广泛应用的高温合金主要是镍基高温合金，随着航空工业的发展，对飞机发动机涡轮叶片材料的承温能力提出了更高的要求。然而，由于传统镍基高温合金熔点的限制，其承温能力的提升极为有限，因此，研发具有更高承温能力的高温结构材料是航空航天的重点研究方向。钴基合金与镍基超合金相比，具有较高的初熔温度(约1450 ℃)、更好的抗热腐蚀和耐磨损性能。然而，由于传统钴基高温合金依靠固溶强化及碳化物弥散强化，缺乏如镍基高温合金中γ′-Ni3Al相(L12结构)类似的强化相，高温强度较低，应用受到限制[1,2]。2006年日本东北大学的石田清仁(K.Ishida)团队[3]首次在Co-Al-W基合金中发现了类似镍基超合金中的L12结构的γ′-Co3(Al, W)有序相，并制备出类似镍基高温合金γ/γ′两相组织的新型钴基高温合金。研究[4,5,6,7]表明，Co-Al-W基合金具有较高的熔点和良好的高温力学性能，有望成为下一代高温结构材料。

然而，新型Co-Al-W基高温合金的研发受到了如下瓶颈问题的限制：(1) Co-Al-W合金的γ′相溶解温度约为1000 ℃[3,8]，远低于镍基高温合金的γ′相溶解温度，极大限制了其承温能力的提升；(2) Co-Al-W合金中的γ′相为亚稳相[9,10,11,12]，在高温长时间保温后，将分解为Co3W等杂相，降低了合金的高温力学性能；(3) Co-Al-W合金具有非常窄的γ/γ′两相成分区域[3]，限制了通过合金化手段来提升合金的综合性能；(4) Co-Al-W合金由于需要添加大量W元素以稳定γ′析出相，使合金的密度急剧增加，制约了该类材料在航空领域的应用[13,14,15]。因此，利用合金化等方法，制备出兼具较高γ′相溶解温度、优异的组织稳定性和较低的合金密度的新型钴基高温合金，是该研究领域亟待解决的重要课题。

近年来，研究者们通过实验方法，对新型钴基高温合金的组织和性能等开展了大量的研究工作。Shinagawa等[16]发现Ni元素的添加使得Co-Al-W合金中的γ′相稳定化，并拓宽合金中的γ/γ′两相成分区域。Omori等[17]的研究结果表明，Ti、Nb和Ta等能显著提升Co-Al-W合金中γ′相的溶解温度，而Cr元素的添加使得γ′相热稳定性降低。研究人员[18,19,20,21,22]通过合金化手段制备出了多元Co-Al-W基高温合金。但到目前为止，科研人员主要是基于“炒菜法”开展相关研究，实验周期长、耗费大，造成极大的人力物力浪费，而且很难找到性能优异的目标合金。

材料基因组工程以及多尺度材料设计理论和计算方法的发展，为新型钴基高温合金的研发提供了新的研究思路。相图计算(calculation of phase diagrams，CALPHAD)方法和第一性原理计算方法作为合金设计的重要手段，实现了人力和物力的节省以及合金的高效设计，已成功应用于镍基高温合金中，并有望在Co-Al-W基合金的高效开发上获得重要应用。通过结合新型钴基高温合金动力学数据库和相场模拟等方法，有望实现新型钴基高温合金的组织控制以及高温服役状态下的组织演变机理研究。此外，耦合机器学习和实验数据的方法已经在新型钴基高温合金的合金设计中获得重要应用，为设计具有高γ′固溶温度和γ/γ′组织稳定性的合金提供理论指导。综上所述，耦合第一性原理计算、CALPHAD、相场模拟及机器学习等手段的多尺度设计方法有望在新型钴基高温合金中实现合金的高效设计。

本文基于本课题组多年来在新型钴基高温合金多尺度设计方面的成果以及国内外学者的研究成果，系统地总结了材料多尺度计算方法在新型钴基高温合金领域的研究现状，其中包括第一性原理、CALPHAD、相场法以及机器学习和数据挖掘技术在合金成分筛选、工艺设计和组织优化领域的多尺度耦合设计。在此基础上，提出了各个尺度研究方法的优势和问题，并对多尺度集成材料设计方法在新型钴基高温合金领域的发展趋势做了展望。

1 基于第一性原理计算的新型钴基高温合金的设计

1.1 第一性原理计算与材料设计

计算机技术的迅猛发展，极大程度地带动了计算机模拟方法的应用。材料的研发可以不再单纯地依靠传统的“试错”实验方法而盲目地添加合金元素。如今，理论计算被认为是可以与实验技术并驾齐驱的科学研究手段，基于密度泛函理论的第一性原理计算方法是目前被广泛地应用于物理、化学、生物及材料等学科专业中的一个计算模拟工具。第一性原理方法是在量子力学理论基础上，不依赖实验数据、经验或者半经验参数，利用基本的物理常量求解薛定谔方程而获得系统能量的计算方法。通过第一性原理计算预测得到材料的基本物理性能如晶格常数、体系结合能、电子结构及弹性性能等，能与实验数据取得非常好的一致性。

与镍基高温合金不同，新型钴基高温合金中γ′析出相为部分短程无序结构的亚稳定相。该相的诸多物理、化学及力学等性质很难通过实验加以测定表征，给进一步优化合金性能带来很多问题。为此，研究者试图借助第一性原理计算方法的精确性和广泛性，从不同合金组分体系入手(例如：二元Co-X体系、三元Co-Al-X体系、三元Co-V-X体系、三元Co-Ta-X体系、三元以上Co-Al-W-X体系等)，理论研究γ′相的结构稳定性、力学性质以及热力学性质，包括部分无序结构模型建立、微量合金结构占位、弹性力学性质、扩散、理想强度以及层错能等，尝试从微观电子信息揭示影响γ′析出相的机理和规律。利用理论计算结果，克服传统“试错”实验手段带来人力物力浪费的弊端，初步建立一套完整的合金设计理论方法，为实验研究过程中的合金成分设计与有效筛选提供有力的理论指导和支撑。

1.2 微量合金与Co基体的相互作用研究

实际应用中，通过添加多种合金元素以改善新型钴基高温合金的性能，往往会得到意想不到的优异性能。而这些合金元素多与合金中Co单质发生物理化学作用，从实验角度同时研究不同微量合金与Co的相互作用影响是不现实的。理论上，通过计算合金元素在Co中的扩散行为，以及在塑性变形行为的层错能影响，可以很好地从原子键合结构角度了解这种物理化学的微观机理。Naghavi等[23,24]和Neumeier等[25]先后研究了Ti、V、Cr、Mn、Fe、Nb、Mo、Ru、Ta、W等多种合金元素在Co中的扩散行为和空位形成能量。研究发现，过渡金属的固溶容易在Co中形成空位，大尺寸原子固溶在Co中，会自发朝着最邻近空位位置移动，以降低晶格畸变应力，从而提高原子的扩散速率。如果固溶原子半径过大，则会在向空位方向移动途中陷入一个能量极小值位置，不容易发生扩散，如图1[24]所示。Re元素尽管在镍基高温合金中起到至关重要的作用，然而在Co中的扩散却非常缓慢，这与Re原子易和临近Co原子发生作用有直接关系[25]。Tian等[26]和Breidi等[27]通过计算Co-X体系的层错能变化，研究微量合金添加对合金塑性变形行为的作用影响。研究表明：Cr、Ru、Rh不利于高温fcc-Co的稳定化；Fe、Ni、Pd则会提高层错能垒，抵抗塑性变形并有利于高温结构稳定性；Mo和W的影响与其添加浓度有关系，当添加浓度较低时，可提高塑性变形层错能垒，若添加浓度超过10% (原子分数)，则会起到相反的作用效果；Ti、Zr、Hf、Nb和Ta有利于Co3Al0.5W0.5结构的稳定化。

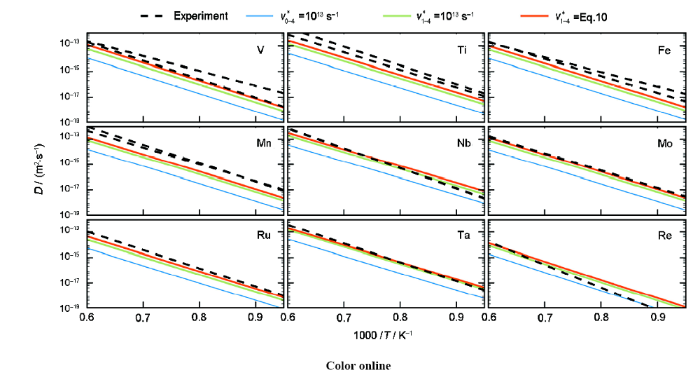
图1   过渡金属元素在fcc-Co中的扩散实验数值与多种近似拟合比较[24]

1.3 二元关键相的性质研究

Sato等[3]和Suzuki等[4,28]的研究不仅表明了Co-Al-W基合金的高温强度优于部分商用镍基高温合金(如Wasploy?)，更重要的是为制备多组元新型钴基高温合金提供了新的研究思路。Sato等[3]认为，几何密排的Co3Al是一个关键相，W添加促使了亚稳定Co3Al发生稳定化，从而发现了γ′-Co3(Al, W)析出相。优化第三成分配比，完全可能使这种几何密排的A3B相稳定化，从而得到新的析出强化型钴基高温合金体系。而据文献[3,29,30,31,32]报道，部分二元Co合金体系中存在稳定或亚稳的L12结构的Co3X相，如Co-X (X=V, Al, Ta, Ti)。针对二元Co3X数据信息不完整的现状，Xu等[33]利用第一性原理方法计算了Co3X (X=Ti, Ta, Al, W, V)的基础平衡态物理信息、弹性力学性质，建立完整的Co3X结构的数据信息。Xu等[34]和Wang等[35,36]建立了一套原子择优占位的热力学分析方法，研究了高达23种的过渡金属在关键二元相Co3Al、Co3V、Co3Ta中的择优占位情况，以及相结构稳定性，如图2[34,35,36]所示。利用应力-应变方法，分析了过渡金属影响Co3Al结构力学性质的机理和规律，并利用准简谐Debye模型建立一套完善的热力学数据库。研究表明：W、Ti、Re、V和Ta原子强烈倾向占据Co3Al中的Al位并可能使Co3Al相结构稳定性，而倾向占据Co位的固溶元素不利于Co3Al的结构稳定性提高。Ti、Ta、Hf、Nb、Zr、Sc和W能够有效稳定L12结构的Co3V化合物。在占据Co位的过渡金属元素中，Ir、Pt、Rh和Ni能有效稳定L12结构的Co3V化合物，而Al、Ti、V、Nb、Mo和W优先选择占据L12和D019结构的Co3Ta化合物中的Co位，Mo的添加有效地提高L12有序相Co3Ta的结构稳定性。另一方面，掺杂元素对Co3Al、Co3V、Co3Ta的力学性质影响呈现出规律性变化趋势，个别原子的异常表现与其微观电子键合分布有直接的关系。Jin等[37]研究了Co3(Al, M) (M=Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, W)在L12和D019结构下的相稳定性，结果表明：Al原子很大程度上提高了L12结构的稳定性，而W原子提高L12结构的力学性能，Cr原子有可能替代W原子而使得L12结构的Co3(Al, Cr)发生稳定化。Wang等[38]借鉴实验和计算手段，研究了固溶原子对L12结构Co3(Al, TM) (TM：Cr, Hf, Mo, Ni, Re, Ru, Ta, Ti, W, Y)的(010)反相畴界能量的影响，结果表明：(010)反相畴界的形成有利于L12 Co3Al结构的稳定化，而固溶原子影响反相畴界能量的顺序为：Mo>W>Re>Cr>Hf>Ti>Y>Ta>Ru>Ni>Al。

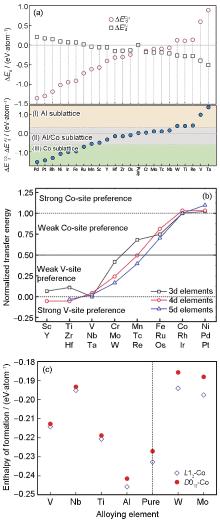
图2   过渡族金属元素分别占据Co3Al 化合物中Al位和Co位对应的反应生成能[34]，元素X在Co3V中的占位倾向图[36]，及L12-Co3(Ta, X)与D019-Co3(Ta, X)化合物的形成焓对比[35]

1.4 三元Co3(Al, W)析出相的性质研究

尽管Sato等[3]和Suzuki等[4,28]的实验报道了析出强化型钴基高温合金的γ′析出相溶解温度高于部分商用镍基高温合金，但其γ′-Co3(Al, W)在900 ℃以上为亚稳相结构，因此，探究合金元素对γ′相的影响机理和规律，以有效地提高γ′析出相结构稳定性，是新型钴基高温合金研究中极为重要的问题之一。Chen和Wang[39,40]通过能量最低方法构建有序L12结构，先后研究了多种过渡金属在γ′-Co3(Al, W)的择优占位和相结构稳定性，结果表明：Ni、Mn、Mo、Ta倾向占据W位置，Ru和Os倾向占据Co位置，其中Mo、Ta、Rh、Ir、Pt、Ni、Fe、V、Ti能提高γ′-Co3(Al, W)的结构稳定性，然而实验表明γ′析出相结构为部分无序结构。Jiang[41]通过特殊准无序方法(special quasi-random structures)，理论构建了一个准无序结构，该结构很好地反映了γ′析出相的结构信息，为后续理论研究提供了结构模型。借助该结构模型，Xu等[42]研究了高温下γ′析出相的力学性质，分析了其力学性质随温度提高而减小的微观机理，并首次建立γ′析出相的熵、焓、热容等热力学数据信息。Xu等[43]还研究了Ta提高γ′-Co3(Al, W)的力学性能的微观本质，发现Ta趋向占据Al位，并使γ′-Co3(Al, W)析出相的自由能降低而更加稳定。在塑性变形过程中，Ta原子与邻近Co、W原子形成了环状金属键，以抵抗塑性变形，提高力学强度，如图3[43]所示。Mottura等[44]和Saal等[45]先后研究了合金元素Ta添加对γ′-Co3(Al, W)的超级内秉层错及反相畴界形成的影响情况，发现Ta的微量添加即可很大程度地提高γ′析出相的内秉层错能，然而内秉层错能提高似乎与屈服异常的情况无关。Saal等[45]认为反相畴界结合能大小依赖于Al、W成分的配比，Al原子倾向在反相畴界处发生偏析。另一方面，合金元素在γ/γ′两相界面处的行为表现，对于理解合金化影响相结构至关重要。Chen和Wang[46]通过构建γ/γ′两相结构，研究了关键元素Re和Ru在相界处的配分行为，发现了Re和Ru均更倾向进入γ基体相，Ru的存在会阻碍Re原子进入γ基体相，而Ru和Re在γ′相中也会一定比例地固溶，且Re倾向占据析出相的W位置而Ru倾向占据析出相的Co位置。

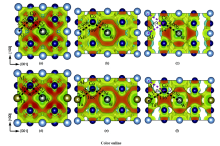
图3   Ta掺杂前后Co3(Al, W)的结构在[001]拉伸作用下的变形电荷差分密度对应的等值面图[43]

1.5 小结

综上所述，借助密度泛函的理论方法，研究者研究了多种过渡金属元素对基体Co、关键二元相、三元析出相的物理化学性质的影响，揭示合金化影响的机理和规律，尝试建立一套完善的热动力学数据信息库，形成高性能新型钴基合金的综合设计系统。基于该综合设计系统，可初步地筛选具有合适成分、相组成及组织形态的新型钴基合金成分、优化实验工艺，以节约实验成本、减少实验周期。

2 基于CALPHAD方法的新型钴基合金热力学数据库的建立及其应用

2.1 CALPHAD方法与材料设计

随着计算材料科学的发展，相图计算，即CALPHAD逐渐成熟，并发展成为一门介于热化学、相平衡和溶液理论与计算技术之间的交叉学科分支，也是材料科学的重要分支。具有实用价值的多元体系热力学数据库的构筑，进一步使CALPHAD方法发展成为多元合金设计的重要工具。随着对高温合金工作温度和力学性能要求的不断提高，高温合金的合金化十分复杂，大部分材料均为多元合金。因此，基于CALPHAD方法进行热力学计算，可分析高温合金的相组成以及每一个组成相的产生和演变过程，在此基础上结合对这些组成相特性的认识，预测高温合金的力学性能和物理性能，进而设计和优化高温合金的成分和工艺。目前，利用在CALPHAD框架下的热力学计算实现高温合金的成分-组织-性能的一体化设计已经成为国内外研究的热点[47,48]，也取得了一定的研究成果，尤其是对镍基高温合金中的研究[49,50]。自20世纪70年代，以美国为代表的一些国家已经把相图计算应用于高温合金的工程生产中，例如，美国通用电气公司(GE)开发的燃气轮机用的GTD262高温合金就是采用材料计算与实验相结合的研究方法，通过热力学计算预测高温合金的组织稳定性，并在材料性能数据库的基础上综合考虑高温合金的性能，对合金进行了优化设计，不仅大大缩短了合金设计到实际生产应用的时间，而且大幅降低了研究开发的成本[51]。Dupin和Sundman[50]基于CALPHAD方法建立了包含Al、Co、Cr、Ni、Re、Ti、W等7种元素的镍基高温合金热力学数据库，该数据库包含21个二元系和若干镍基三元系的热力学参数，对指导镍基高温合金的设计发挥了重要作用。

相比于镍基高温合金，新型钴基高温合金的合金化研究还十分有限，包括如何通过合金化获得γ+γ′两相组织，怎样通过合金化获得热力学稳定性更好、强度更高的γ′相等。而相图作为合金相平衡关系的状态图，是合金化研究的重要工具，特别是利用相图热力学计算与实验测定结合的方法指导材料设计是目前最高效的合金设计方法，对具有一定组织和性能的多组元或多相材料的成分具有预见性，成为预测外推多元系相图方面不可替代的重要方法。当前，研究者们已经对新型钴基高温合金体系的热力学计算开展了卓有成效的研究工作。例如，东北大学蒋敏团队[52]建立了5个组元的新型钴基高温合金热力学数据库，北京科技大学杜振民研究团队[53,54,55]也评估了若干个新型钴基高温合金体系的相图。本课题组[56,57,58,59,60,61,62,63,64,65,66]针对新型Co-Al-W基高温合金中的重要合金化元素Co、Al、W、Ni、Ta、Ti、Cr开展了相图的实验研究和热力学计算。

2.2 新型钴基高温合金热力学数据库的建立

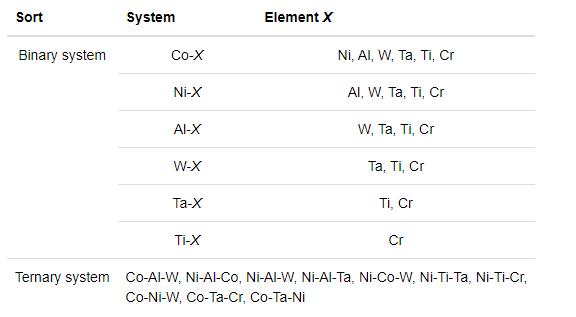
近年来，本课题组[56,57,58,59,60,61,62,63,64,65,66]利用相图计算的CALPHAD方法，结合相平衡和热力学性质的相关实验数据，对Co-Ni-Al-W-Ta-Ti-Cr二元系以及三元系相图进行了热力学优化与计算，初步建立了新型钴基合金的热力学数据库。该数据库的热力学优化与计算工作是在Sundman等[67]开发的Thermo-Calc软件上完成的，其中液相和端际固溶体相的Gibbs自由能采用亚规则溶体模型来描述，金属间化合物相的Gibbs自由能采用亚点阵模型来描述，液相热力学参数的评估主要依据相平衡的实验数据和液相混合焓、液相自由能、活度等热力学性质的实验数据，而固相热力学参数的评估则主要依据于相平衡的实验信息和熵、焓等热力学性质的实验结果，通过Thermo-Calc软件上的PARROT模块进行优化，使得计算结果与实验值取得良好的一致性，最终获得合理地描述二元和三元系中各相自由能的热力学参数。在获得所有基础二元系和基础三元系热力学数据库的基础上，充分考虑热力学模型的统一性和热力学参数的兼容性，建立Co-Ni-Al-W-Ta-Ti-Cr多元系热力学数据库，该数据所包含的合金体系如表1所列。

表1   新型钴基高温合金热力学数据库

2.3 新型钴基高温合金的组织设计

新型钴基高温合金的相组成与合金的性能密切相关，因此，基于本课题组开发的新型钴基合金系热力学数据库，通过计算新型钴基合金的相平衡关系和随温度相分数的变化可实现新型钴基高温合金的组织设计。图4表示Co-Al-W三元系实验相图等温截面[3]和Co-Al-W-xNi (x=10、20、30)在900 ℃时的伪三元截面相图。值得一提的是，该计算等温截面相图与Shinagawa等[16]报道的Co-Ni-Al-W实验相图具有良好的一致性，表明当前的热力学数据库具有较好的精度。由图可知，Co-Al-W三元系相图中，γ+γ′两相成分区域较窄，一方面使得γ+γ′两相合金的成分控制更加困难，另一方面制约了合金通过合金化手段提升综合性能的可能性。然而，由图4和5可知，随着Ni含量的增加，合金中的γ′相稳定化，γ+γ′两相成分区域不断扩大，这为后续合金化元素添加提供了更大的可能性。除此之外，这为Co-Al-W基合金的发展提供了新思路，即通过添加大量的Ni元素使得γ′相稳定化，并拓宽γ+γ′两相成分区域，从而设计并制备出复合合金化的高性能新型钴基高温合金。

图4   Co-Al-W三元系在900 ℃时的等温截面相图[3]及计算的Co-Al-W-xNi四元系在900 ℃时的伪三元等温截面相图

由于Cr元素是高温合金的必要元素，Cr元素的添加对合金的抗氧化和抗腐蚀性能的提升起到至关重要的作用[1,2]。然而，Cr元素的添加急剧降低了合金中γ′相的热力学稳定性[6,17,22,28]，因此，如何设计出兼具较高γ′相热稳定性和良好抗氧化能力的Co-Al-W基高温合金是该领域亟待解决的重要问题之一。图6所示为本课题组计算的Co-Ni-Al-W-Cr合金在900 ℃时的等温截面相图。由图可知，当Cr添加量为15% (原子分数)时，随着Ni含量的增加，合金中的γ+γ′两相成分区域不断变宽，而且γ+γ′两相成分区域向高Al成分移动。

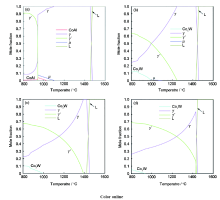
图5   计算的Co-10Al-10W、Co-10Al-10W-10Ni、Co-10Al-10W-20Ni和Co-10Al-10W-30Ni合金的相分数曲线

图6   计算的Co-xNi-Al-W-15Cr合金在900 ℃时的等温截面相图

2.4 小结

目前已经初步建立了新型钴基高温合金热力学数据库。但由于新型钴基高温合金的熔点高、熔化困难以及平衡化热处理时间长等问题，对新型钴基高温合金重要体系的相图研究还不充分，需要通过实验进行系统地研究。在实验数据的基础上，利用CALPHAD技术，通过选择和建立合理的热力学模型，并解决由于存在着热力学模型不统一和热力学参数不兼容等问题，才能建立较为精准的新型钴基合金多元系热力学数据库。

3 新型钴基合金动力学数据库及其在相场中的应用

3.1 动力学相场模拟与材料设计

高温合金的力学性能属于组织敏感型性能，合金的成分分布、相分布及组织形貌都会对力学性能产生影响。仅依靠热力学计算分析成分及物相组成难以满足合金设计的需求，因此需要结合动力学计算定量分析不同工艺过程中由扩散控制的现象(如微观偏析、析出相的长大与溶解等)。作为动力学计算的基础——扩散系数的计算与评估，动力学数据库的建立与完善是非常重要的，也是实现材料组织相场模拟的基础参数。因此，基于热力学数据库与动力学数据库，可定量分析新型钴基合金凝固与热处理过程中由扩散控制的现象，如成分均匀化、微观偏析、析出相的长大与溶解等。结合相场法，可动态模拟新型钴基合金中析出相的分布、取向等随工艺条件的变化情况，为通过成分与工艺设计实现新型钴基合金性能的改进提供了直接指导。

相较于热力学数据库，新型钴基高温合金体系的动力学数据库的研究工作相对有限，且集中于fcc相。Gómez-Acebo等[68]建立了Al-Co-Cr-Ni-Ti体系中fcc相的动力学数据库。一些学者评估了部分重要体系(如Co-Al-W、Co-Cr-Ni、Co-Cr-V等)中fcc相的扩散系数[69,70,71,72,73,74,75,76,77]。近年来，本课题组利用第一性原理和半经验公式，对合金体系中未知的自扩散和杂质扩散系数进行了预测，采用基于CALPHAD方法的DICTRA软件，结合相关扩散数据，对Co-Ni-Al-W-Ta-Ti-Cr二元系以及三元系的互扩散系数进行了评估，初步建立了fcc相新型钴基合金的动力学数据库。

通过相场法耦合高温合金热力学与动力学数据库是设计高温合金的重要手段之一。相场法的发展为直观研究高温合金中的相变机理及微观组织转变规律对合金综合性能的提升具有重要意义[3,78]。利用现代计算机的超级计算能力，相场法可求解包含弹性场、温度场、浓度差的复杂动力学方程(图7)，模拟得到真实的微观组织结构演变。

图7   合金设计与模拟过程

目前国内外学者对高温合金相场模拟的研究大多集中在镍基高温合金，主要在其凝固过程、时效热处理、应力蠕变等几方面，并利用现有完善的镍基高温合金数据库开展了一系列组织演化模拟工作[79,80]。在时效热处理方面，研究者可以通过相场模拟研究时效温度、合金成分和错配度等因素对γ′相的形貌、粒径分布以及其粗化行为等的影响，从而确立最佳合金成分和热处理工艺，达到提高合金性能的目的[81,82,83]。在应力蠕变方面，高温合金在外加载荷条件下会出现筏化行为，而筏化行为将会降低其蠕变疲劳寿命。因此，结合理论计算和实验研究合金中γ′颗粒筏化行为，将有助于深入了解高温合金的失效机理[84,85,86]。

针对新型钴基高温合金的微观组织演变相场模拟，国内外学者也已经开始了一定的研究。高一鹏等[87]采用相场方法定性模拟了Co-Al-W合金中γ′相组织演变的影响，得到与实验结果相符的组织结构。Koyama[88]运用相场法定性模拟Co-9Al-7.8W合金和γ′体积分数为0.7时Co-Al-W-Ta时效析出过程。Jokisaari等[89]对Co-9.1Al-5.3W合金的单个和多个沉淀相颗粒进行三维模拟，研究弹性能和界面能对粗化和筏化微观结构的影响，并观察到沉淀相颗粒的微观特征结构取决于施加应力的类型，以及共格界面产生的弹性应力场是改变蠕变过程中形态的关键因素。

3.2 新型钴基高温合金动力学数据库的建立

自扩散系数与杂质扩散系数是构建动力学数据库的重要部分，采用同位素示踪法可获得稳态下体系的自扩散与杂质扩散系数，但是难以确定亚稳态下体系的扩散系数，从而阻碍了相关动力学数据库的建立。为此，研究者多采用第一性原理、机器学习和半经验公式等方法对难以通过实验获得的自扩散与杂质扩散系数进行预测。Shang等[90]采用第一性原理的方法计算了元素周期表中大部分元素在fcc、bcc和hcp结构中的自扩散系数，部分计算结果因非简谐效应而与实验结果之间存在较大偏差，或因收敛性问题而出现无法完成计算的情况。本课题组[91]通过第一性原理计算结果，修正了Dushman等提出的预测模型[92]，并计算了Al、Nb、Zn等元素在fcc、bcc和hcp结构中的自扩散系数。对比实验结果，采用修正后预测模型计算的结果展现出较好的匹配程度，如图8[91]所示。Mantina等[93]和Hargather等[94]采用第一性原理的方法分别计算了铝基和镍基合金在fcc中的杂质扩散系数，计算结果与实验数据保持了较好的一致性。Zeng等[95]与Wu等[96]采用机器学习方法预测了fcc二元体系中杂质扩散系数。本课题组则基于修正后的预测模型，预测了金属体系的杂质扩散系数，与实验结果的匹配程度较好，如图9所示。

图8   Al和Nb在bcc、fcc和hcp相的自扩散系数[91]

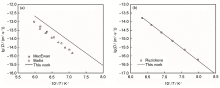
图9   Ni和W在fcc Co的杂质扩散系数

此外，互扩散系数的评估是提升多元动力学数据库的精准度关键，一般采用扩散偶法，结合电子探针(EPMA)微区分析技术和Den Broeder方法或Whittle-Green方法直接测定计算获得相关的互扩散系数。针对Co-Ni-Al-W-Ta-Ti-Cr多元体系在fcc中的扩散行为的研究，本课题组开展了一定的研究工作(如图10[97]所示)[66,97,98]，并初步建立了新型钴基高温合金的fcc相动力学数据库。

图10   1473 K时Co-Cr-Mo三元体系富Co侧互扩散系数()计算值与实验值对比，及扩散路径计算值与实验值对比[97]

3.3 基于相场法的新型钴基高温合金微观组织模拟

本课题组通过耦合热/动力学数据库和相场法，建立了针对新型钴基高温合金中γ/γ′两相组织演化的相场动力学模型，并基于热/动力学数据库，开展了Co-Al-W合金时效过程中微观组织演化的计算机模拟，探讨了初始成分、两相错配度和时效温度等工艺条件对合金时效两相的形貌、体积分数、粗化速率、筏化行为等组织特征的影响，模拟结果中的γ′体积分数、γ体积分数各元素浓度分布和粗化速率与实验结果符合良好，为新型钴基高温合金的组织设计和工艺优化提供重要的理论依据。

本课题组基于新型钴基高温合金Co-Al-W (图11)等一系列合金开展了组织演化模拟，分析了其组织演化过程γ′相体积分数、颗粒数、平均颗粒半径等，并与实验取得了良好的一致性。同时，如图12所示，还考虑了定向应力对组织演变的蠕化作用，探讨了外应力对不同γ′相体积分数Co-Al-W合金的影响，在外加应力作用下，Co-9.0Al-9.0W合金中γ′颗粒粗化速率的增大程度大于Co-9.2Al-9.5W合金中γ′颗粒粗化速率的变化，说明了γ′相体积分数增大，对于受外加应力的影响会相对较小。目前相关实验研究[99]也表明，γ′相体积分数为60%以上的合金比γ′相体积分数为40%的合金具有更高蠕变强度。

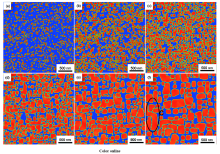
图11   Co-9.0Al-9.0W合金在900 ℃ γ‘析出相随时效时间的组织演变模拟图

图12   外加应力下Co-9.0Al-9.0W合金在900 ℃ γ’相随时间的组织演变模拟图

由于Co-Al-W体系的高温合金在时效后期出现γ′不稳定现象，这可能是γ′在新型钴基高温合金的一种特殊亚稳相形态。在这种情况下，本课题组在两相演变基础上，扩充模拟体系，向体系内添加第三相(例如D019)来研究γ‘相溶解的演化过程，如图13所示。其模拟结果不但可以观察D019相在时效后期析出长大的过程，而且还可以分析γ’相在体积分数减少的情况下，其粗化机理和粒径分布规律。在相场法研究新型钴基高温合金中，拓宽了研究视角，为材料设计提供了更多有价值的信息。

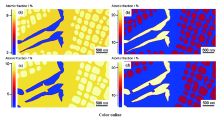
图13   Co-9.3Al-10.5W合金晶界处γ‘、γ、D019三相在900 ℃随时间的组织演变模拟图

3.4 小结

目前为止，新型钴基多元高温合金动力学数据库依旧需要进一步完善。首先，采用Whittle-Green等方法计算互扩散系数的效率相对较低，高通量计算互扩散系数的方法需要进一步改进与应用。其次，现有动力学数据库的研究重点多集中于fcc、bcc和hcp相，而实际合金中所涉及的物相不局限于固溶体，因此动力学数据库尚需进一步完善。

本课题组已针对Co-Ti、Co-V、Co-Ta几种二元系新型钴基高温合金进行了研究，接下来将继续对现有已开发出的Co-Al-W、Co-V-Ti、Co-Ni-Al-W等多元合金系进行深入探究，并利用第一性原理所计算出的界面参数以及已建立的成熟热力学和动力学数据库，进行模拟探索合适的热处理工艺和合金的成分配比。通过相场法了解影响新型钴基高温合金微观结构演化的因素，提供优化元素配比的依据，将为加速开发新型钴基高温合金起到重要作用。

4 基于机器学习算法的新型钴基高温合金快速设计

4.1 人工智能技术与材料设计

与其它种类的材料相比，高温合金的制备与测试耗时更长。以Co-Al-W合金为例，为了确定其γ’强化相是否稳定，需要将样品加热至900 ℃以上保温超过2000 h。因此，为了加速高温合金的设计，急需寻找新的设计方法。在高温合金研究过程中，上文提到的CALPHAD法与第一性原理计算方法都是基于材料学理论的计算材料学方法。除此之外，还可以使用数值拟合方法进行材料设计。

采用数值拟合结合高通量计算的高温合金设计思路最早由Morinaga等[100]提出。在研究镍基高温合金的过程中，他们发现镍基高温合金中的杂相是否析出与合金中元素的电负性及原子半径有关。与此同时，元素的电子轨道参数Md也与以上两者相关。据此，Morinaga等[100]尝试并发现了镍基高温合金的多种微观组织参数与Md的定量关系，并据此对多种高温合金设计方案进行筛选，最终成功制备了一种新型镍基高温合金。这种利用元素微观信息与合金组织定量关系进行高温合金设计的高通量方法被称作PHACOMP，即相图计算法。然而，此种方法也存在一定的局限性。PHACOMP方法仅仅适用于进行镍基高温合金的设计工作，在进行新型钴基高温合金设计时会产生较大的误差，这可能是因为PHACOMP采用的数据分析方法仅仅是简单的线性回归方法。为此，需要采用其它数学模型对高温合金数据进行分析，而机器学习算法恰好适合解决此类问题。

机器学习算法属于人工智能范畴，是使计算机实现自我学习的算法。机器学习算法被广泛应用于数据挖掘领域，即尝试在数据库中计算机自发地发现新知识的过程。利用机器学习算法，可以建立描述材料成分-工艺-组织-性能间定量关系的数学模型，为材料的设计提供指导思路。随着近年来人工智能技术的兴起，采用智能算法进行材料研发也逐渐得到重视。目前，机器学习算法已经被成功地应用于压电材料、非晶材料、传统结构材料等材料体系的设计工作中。如Fischer等[101]利用结构之间的关联性发展了数据挖掘结构预测的方法，并成功实现了Ag-Mg合金的基态结构预测。Ren等[102]将机器学习算法和高通量实验方法结合起来，对非晶玻璃进行了快速设计。2016年，《Nature》发表了2篇采用人工智能技术进行材料设计的相关封面文章。其中一篇文章对材料信息学的发展过程做了系统讲述[103]，另外一篇文章则是利用先进的机器学习算法对实验中失败的数据进行了分析，并利用他们学习到的模型对新材料的合成做出了预测，发现模型的预测准确率比人工的预测准确率要高出20%[104]。这2篇文章都对与信息学相结合的新材料研究方法做出了高度评价，并预言这将会是以后材料研究的主流方法。在高温合金领域，郭建亭等[105]采用人工神经网络算法建立了镍基高温合金蠕变寿命的预测模型，然而在新型钴基高温合金领域相关文献报道还很少。为此，本课题组[106]采用机器学习算法进行了新型钴基高温合金的设计尝试。

4.2 新型钴基高温合金γ‘相稳定性优化设计

本课题组研究工作的整体框架如图14[106]所示。首先通过文献采集、实验数据收集等方式建立了新型钴基高温合金数据库，数据库中有近500条信息，包含了合金的成分、工艺条件、微观结构与性能的相关信息。

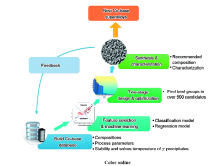
图14   基于机器学习算法的新型钴基高温合金高通量设计方法构架图[106]

之后，采用目前主流的机器学习算法(人工神经网络、支持向量机、随机森林等[107,108,109])对数据进行了挖掘，建立了描述高温合金γ’稳定性与γ‘固溶温度和成分、工艺定量关系的数学模型。各模型的精度如图15[106]所示。图中，横坐标为预测数据的真实值，纵坐标为模型的预测值。当预测值等于真实值时，数据会分布在图中的45°虚线上。因此，点越集中分布在虚线上，模型预测效果越好。可以看出，人工神经网络和随机森林的预测点较为集中地分布在虚线两侧。此外，也采用了数据评估指标对模型进行了评估。所采用的评估指标有相关系数(R)、判定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)，各个模型的评估指标，如图16[106]所示。

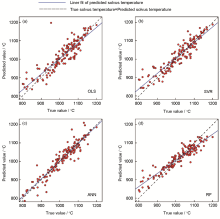
图15   各算法(最小二乘法、支持向量机、人工神经网络及随机森林)对新型钴基高温合金γ’固溶温度的预测情况[106]

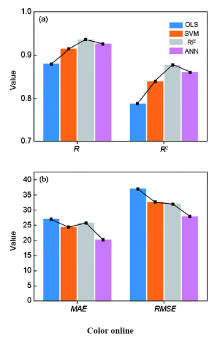
图16   各个模型的评估指标数值[106]

对不同算法建立的数学模型的精度进行考量之后，选择具有最高精度的随机森林模型进行了新型钴基高温合金的高通量设计工作。通过对超过400组的高温合金设计方案进行筛选，最终确定了4种设计方案，如图17a[106]所示。实验结果[106]表明，2Nb高温合金的γ‘固溶温度为1135 ℃，高于Omori等[17]报道的Co-8.8Al-9.8W-2X (X=Ti、V、Nb、Ta)四元合金的γ’固溶温度，计算结果与实验测试结果如图17b[17,106]所示。优化的合金的微观组织均具有高体积分数的γ‘相，且γ’相为规则的立方状，如图18[106]所示。

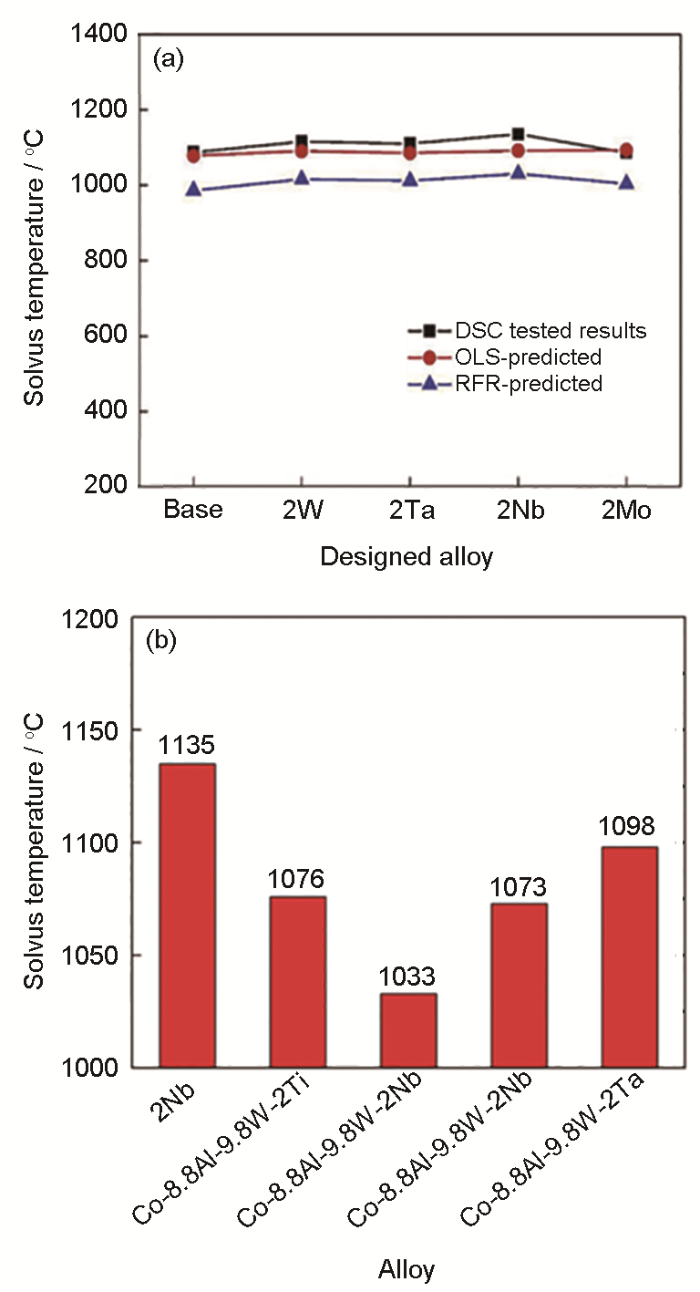
图17   4种新成分的新型钴基高温合金γ‘固溶温度随机森林模型预测值与差示扫描量热法实验测试值[106]，及本课题组制备的2Nb合金[106]与Co-8.8Al-9.8W-2X (X: Ti, V, Nb, Ta)合金γ’固溶温度[17]对比图

图18   基于机器学习算法的新型钴基高温合金快速设计得到的高温合金组织图[106]

4.3 小结

以上结果表明，机器学习算法可以有效地加速新型钴基高温合金的设计工作。然而，目前仍有部分问题需要解决。首先是高温合金的数据来源问题，上述研究中使用的数据来源中有大半来源于文献数据，然而发表的文献往往仅包含性能较好的合金信息，“不成功的”合金数据并不会被发表。因此，需要建立新型钴基高温合金的科研数据共享平台，加速数据积累。此外，在模型对合金进行了预测后仍需要进行实验验证。因此，需要发展新型钴基高温合金的高通量测试方法，加速合金设计。

5 新型钴基高温合金多尺度设计的展望

对于新型钴基高温合金体系而言，其多组元的特性增加了材料设计的复杂性。而单一尺度量级的模型都包含不同程度固有的局限性，如精度或者维度无法满足实际情况的要求。新型钴基高温合金是个十分复杂的材料体系，其微观结构对宏观性能有着重要影响。为了获得精度更高、更能反映材料本征属性的结果，基于原子结构和电子能量的第一性原理(包括第一性原理分子动力学)计算是目前广泛采用的一种方法。然而，在整个系统上使用微观尺度量级的模型，一方面在空间尺度上无法建出反映实际情况的模型(包含多组元、多晶、多相、缺陷)，就算勉强建出也由于计算量过大而无法进行。另一方面在时间尺度上无法跨越微秒量级的限制(同样由于计算量过大)，一些演化规律与长时间有关的性质不能准确给出。而再往上一个尺度的经典分子动力学或Monte Carlo模拟虽然在空间尺度和时间尺度上较第一性原理方法有很大程度的提高，但它们都依赖势函数的准确性。目前，能够准确描述多组元新型钴基高温合金原子间相互作用力的势函数还很缺乏。因此，单独采用经典分子动力学或Monte Carlo模拟方法也缺乏实用性。最后，能够较为直接反映材料宏观性质和动力学行为的介观模拟(如粗粒化经典分子动力学、相场法或Monte Carlo模拟)或是有限元方法则依赖大量的经验参数，且不具有普适性，实际操作起来存在很大困难。由此可见，为了满足新型钴基高温合金材料成分、性能和工艺方面的需求，基于多尺度模拟的复杂设计系统的开发迫在眉睫。

第一性原理计算、CALPHAD方法和相场模拟作为新型钴基高温合金多尺度合金设计的重要环节，可实现人力和物力的节省以及合金的高效设计，已成功应用于镍基高温合金中，并有望在Co-Al-W基合金的高效开发上获得重要应用。与镍基高温合金类似，新型钴基高温合金体系热/动力学数据库是合金成分设计的重要依据。但目前缺乏基础的热力学以及动力学数据，商用数据库的精度不足，并且不具有可扩展性。将来可通过采用第一性原理和分子动力学方法对热力学性质进行高通量优化，并基于热力学/动力学模型和实验数据，开展相图和原子迁移率的优化计算，以保证热力学和动力学数据库的精度，解决合金设计的有效性和可靠性的问题。同时，可以耦合机器学习和实验研究手段的方法对利于实现目标性能的元素进行筛选，降低整个设计系统的计算量。

针对新型钴基高温合金的组织特点以及合金综合性能的快速优化设计问题，在建立了合金基础组元数据库及相组成实验数据之后，可采用并行加速相图优化技术，建立合金的多组元热力学和扩散动力学数据库。不仅如此，通过结合新型钴基高温合金动力学数据库和相场模拟等方法，有望实现新型钴基高温合金的组织控制以及高温服役状态下的组织演变机理研究。最终发展基于新型钴基高温合金特点的第一性原理、分子动力学、相图计算、相场模拟和有限元方法等多尺度计算模型耦合的方法，构建高通量多尺度集成设计平台。通过对第一性原理、分子动力学、相图计算、相场模拟和有限元方法等多尺度材料计算软件的并行化，统一多尺度模型输入/输出接口，实现数据共享，并开发任务调度和资源管理系统，建立新型钴基高温合金的高通量多尺度集成设计平台，开展包括热化学、物性数据、晶体结构、缺陷、相图、微观组织和力学性能的多尺度耦合优化设计和高通量并发计算，并结合高通量实验数据对平台的可靠性进行验证，为后续的候选合金设计及实验研究奠定基础。综上所述，耦合CALPHAD、第一性原理计算、机器学习、材料动力学及相场模拟等手段的多尺度设计方法有望在新型钴基高温合金中实现合金的高效设计。

参考文献

[1] Sims C T, Stoloff N S, Hagel W C. Superalloys II [M]. New York: John Wiley & Sons, 1987: 1

[2] Reed R C. The Superalloys Fundamentals and Applications [M]. Cambridge: Cambridge University Press, 2006: 1

[3] Sato J, Omori T, Oikawa K, et al. Cobalt-base high-temperature alloys [J]. Science, 2006, 312: 90

[4] Suzuki A, Denolf G C, Pollock T M. Flow stress anomalies in γ/γ′ two-phase Co-Al-W-base alloys [J]. Scr. Mater., 2007, 56: 385

[5] Pollock T M, Dibbern J, Tsunekane M, et al. New Co-based γ/γ′ high-temperature alloys [J]. JOM, 2010, 62(1): 58

[6] Titus M S, Suzuki A, Pollock T M. Creep and directional coarsening in single crystals of new γ/γ′ cobalt-base alloys [J]. Scr. Mater., 2012, 66: 574

[7] Suzuki A, Inui H, Pollock T M. L12-strengthened cobalt-base superalloys [J]. Annu. Rev. Mater. Res., 2015, 45: 345

[8] Shinagawa K, Omori T, Oikawa K, et al. Ductility enhancement by boron addition in Co-Al-W high-temperature alloys [J]. Scr. Mater., 2009, 61: 612

[9] Kobayashi S, Tsukamoto Y, Takasugi T, et al. Determination of phase equilibria in the Co-rich Co-Al-W ternary system with a diffusion-couple technique [J]. Intermetallics, 2009, 17: 1085

[10] Tsukamoto Y, Kobayashi S, Takasugi T. The stability of γ'-Co3(Al, W) phase in Co-Al-W ternary system [J]. Mater. Sci. Forum, 2010, 654: 448

[11] Lass E A, Williams M E, Campbell C E, et al. γ′ Phase stability and phase equilibrium in ternary Co-Al-W at 900 ℃ [J]. J. Phase Equilib. Diffus., 2014, 35: 711

[12] Lass E A, Grist R D, Williams M E. Phase equilibria and microstructural evolution in ternary Co-Al-W between 750 and 1100 ℃ [J]. J. Phase Equilib. Diffus., 2016, 37: 387

[13] Zenk C H, Povstugar I, Li R, et al. A novel type of Co-Ti-Cr-base γ/γ′ superalloys with low mass density [J]. Acta Mater., 2017, 135: 244

[14] Bocchini P J, Sudbrack C K, Sauza D J, et al. Effect of tungsten concentration on microstructures of Co-10Ni-6Al-(0, 2, 4, 6) W-6Ti (at%) cobalt-based superalloys [J]. Mater. Sci. Eng., 2017, A700: 481

[15] Bocchini P J, Sudbrack C K, Noebe R D, et al. Effects of titanium substitutions for aluminum and tungsten in Co-10Ni-9Al-9W (at%) superalloys [J]. Mater. Sci. Eng., 2017, A705: 122

[16] Shinagawa K, Omori T, Sato J, et al. Phase equilibria and microstructure on γ′ phase in Co-Ni-Al-W system [J]. Mater. Trans., 2008, 49: 1474

[17] Omori T, Oikawa K, Sato J, et al. Partition behavior of alloying elements and phase transformation temperatures in Co-Al-W-base quaternary systems [J]. Intermetallics, 2013, 32: 274

[18] Xue F, Li Z Q, Feng Q. Mo effect on the microstructure in Co-Al-W-based superalloys [J]. Mater. Sci. Forum, 2010, 654-656: 420

[19] Feng G, Li H, Li S S, et al. Effect of Mo additions on microstructure and tensile behavior of a Co-Al-W-Ta-B alloy at room temperature [J]. Scr. Mater., 2012, 67: 499

[20] Xue F, Zhou H J, Ding X F, et al. Improved high temperature γ′ stability of Co-Al-W-base alloys containing Ti and Ta [J]. Mater. Lett., 2013, 112: 215

[21] Povstugar I, Choi P P, Neumeier S, et al. Elemental partitioning and mechanical properties of Ti-and Ta-containing Co-Al-W-base superalloys studied by atom probe tomography and nanoindentation [J]. Acta Mater., 2014, 78: 78

[22] Titus M S, Eggeler Y M, Suzuki A, et al. Creep-induced planar defects in L12-containing Co-and CoNi-base single-crystal superalloys [J]. Acta Mater., 2015, 82: 530

[23] Naghavi S S, Hegde V I, Saboo A, et al. Energetics of cobalt alloys and compounds and solute-vacancy binding in fcc cobalt: A first-principles database [J]. Acta Mater., 2017, 124: 1

[24] Naghavi S S, Hegde V I, Wolverton C. Diffusion coefficients of transition metals in fcc cobalt [J]. Acta Mater., 2017, 132: 467

[25] Neumeier S, Rehman H U, Neuner J, et al. Diffusion of solutes in fcc Cobalt investigated by diffusion couples and first principles kinetic Monte Carlo [J]. Acta Mater., 2016, 106: 304

[26] Tian L Y, Lizárraga R, Larsson H, et al. A first principles study of the stacking fault energies for fcc Co-based binary alloys [J]. Acta Mater., 2017, 136: 215

[27] Breidi A, Allen J, Mottura A. First-principles calculations of thermodynamic properties and planar fault energies in Co3X and Ni3XL12 compounds [J]. Phys. Status Solidi, 2017, 254: 1600839

[28] Suzuki A, Pollock T M. High-temperature strength and deformation of γ/γ′ two-phase Co-Al-W-base alloys [J]. Acta Mater., 2008, 56: 1288

[29] Drapier J M, De Brouwer J L, Coutsouradis D. Refractory metals and intermetallic precipitates in cobalt-chromium [J]. Cobalt, 1965, 27: 59

[30] Peters E T, Tanner L E. A new high-temperature form of the intermetallic compound Co3V [J]. Metall. Trans. Soc. AIME, 1965, 233: 2126

[31] Blaise J M, Viatour P, Drapier J M. On the stability and precipitation of the Co3Ti phase in Co-Ti alloys [J]. Cobalt, 1970, 49: 192

[32] Aoki Y, Asami K, Yamamoto M. Transformation temperatures and magnetic properties of the ordered hexagonal VCo3 compound [J]. Phys. Status Solidi, 1974, 23: K167

[33] Xu W W, Han J J, Wang Z W, et al. Thermodynamic, structural and elastic properties of Co3X (X=Ti, Ta, W, V, Al) compounds from first-principles calculations [J]. Intermetallics, 2013, 32: 303

[34] Xu W W, Shang S L, Wang C P, et al. Accelerating exploitation of Co-Al-based superalloys from theoretical study [J]. Mater. Des., 2018, 142: 139

[35] Wang C P, Yan L H, Han J J, et al. Effects of alloying elements on the structural, elastic and thermodynamic properties of Co3Ta compounds from first-principles calculations [J]. J. Alloys Compd., 2017, 726: 490

[36] Wang C P, Deng B, Xu W W, et al. Effects of alloying elements on relative phase stability and elastic properties of L12 Co3V from first-principles calculations [J]. J. Mater. Sci., 2018, 53: 1204

[37] Jin M, Miao N H, Zhao W Y, et al. Structural stability and mechanical properties of Co3(Al, M) (M=Ti, V, Cr, Zr, Nb, Mo, Hf, Ta, W) compounds [J]. Comp. Mater. Sci., 2018, 148: 27

[38] Wang W Y, Xue F, Zhang Y, et al. Atomic and electronic basis for solutes strengthened (010) anti-phase boundary of L12 Co3(Al, TM): A comprehensive first-principles study [J]. Acta Mater., 2018, 145: 30

[39] Chen M, Wang C Y. First-principles investigation of the site preference and alloying effect of Mo, Ta and platinum group metals in γ′-Co3(Al, W) [J]. Scr. Mater., 2009, 60: 659

[40] Chen M, Wang C Y. First-principle investigation of 3d transition metal elements in γ′-Co3(Al, W) [J]. J. Appl. Phys., 2010, 107: 093705

[41] Jiang C. First-principles study of Co3(Al, W) alloys using special quasi-random structures [J]. Scr. Mater., 2008, 59: 1075

[42] Xu W W, Han J J, Wang Y, et al. First-principles investigation of electronic, mechanical and thermodynamic properties of L12 ordered Co3(M, W)(M= Al, Ge, Ga) phases [J]. Acta Mater., 2013, 61: 5437

[43] Xu W W, Wang Y, Wang C P, et al. Alloying effects of Ta on the mechanical properties of γ' Co3(Al, W): A first-principles study [J]. Scr. Mater., 2015, 100: 5

[44] Mottura A, Janotti A, Pollock T M. A first-principles study of the effect of Ta on the superlattice intrinsic stacking fault energy of L12-Co3(Al, W) [J]. Intermetallics, 2012, 28: 138

[45] Saal J E, Wolverton C. Energetics of antiphase boundaries in γ′ Co3(Al, W)-based superalloys [J]. Acta Mater., 2016, 103: 57

[46] Chen M, Wang C Y. First-principles study of the partitioning and site preference of Re or Ru in Co-based superalloys with γ/γ′ interface [J]. Phys. Lett., 2010, 374A: 3238

[47] Lu X G, Wang Z, Cui Y W, et al. Computational thermodynamics, computational kinetics and materials design [J]. Chin. Sci. Bull., 2013, 58: 3656

[47] (鲁晓刚, 王 卓, Cui Y W等. 计算热力学、计算动力学与材料设计 [J]. 科学通报, 2013, 58: 3656)

[48] Feng W F, Wang Q C, Zhang L. Calculation during material design, A new tendency in material design [J]. Mater. Sci. Technol., 2000, 8(4): 57

[48] (冯武锋, 王春青, 张 磊. 材料设计的发展新趋势—材料设计计算方法 [J]. 材料科学与工艺, 2000, 8(4): 57)

[49] Wang X, Zhu L L, Fang J, et al. Applications of "Materials Genome Engineering" based methods in nickel-based superalloys [J]. Sci. Technol. Rev., 2015, 33(10): 79

[49] (王 薪, 朱礼龙, 方 姣等. 基于“材料基因组工程”的3种方法在镍基高温合金中的应用 [J]. 科技导报, 2015, 33(10): 79)

[50] Dupin N, Sundman B. A thermodynamic database for Ni-base superalloys [J]. Scand. J. Metall., 2001, 30: 184

[51] Jiang L, Zhao J C, Feng G J, et al. Nickel-containing alloys, method of manufacture thereof and articles derived thereform [P]. US Pat, 006945OA1, 2005

[52] Yang S Y, Jiang M, Wang L. Applications of thermodynamic calculations of phase diagrams to new-type Co-based superalloy design [J]. J. Mater. Metall., 2011, 10: 278

[52] (杨舒宇, 蒋 敏, 王 磊. 相图热力学计算在新型钴基高温合金设计中的应用 [J]. 材料与冶金学报, 2011, 10: 278)

[53] Du Z M, Lü D X. Thermodynamic modeling of the Co-Ni-Y system [J]. Intermetallics, 2005, 13: 586

[54] Zhang Y B, Li C R, Du Z M, et al. The thermodynamic assessment of the ternary Co-Ni-Sb system [J]. Calphad, 2009, 33: 405

[55] Li C G, Zhu D M, Zhang Y B, et al. Thermodynamic assessment of the Co-Fe-Sb system [J]. Calphad, 2014, 47: 23

[56] Ruan J J, Liu X J, Yang S Y, et al. Novel Co-Ti-V-base superalloys reinforced by L12-ordered γ′ phase [J]. Intermetallics, 2018, 92: 126

[57] Liu X J, Yu Y, Liu Y H, et al. Experimental investigation and thermodynamic calculation of the phase equilibria in the Co-Cu-V ternary system [J]. J. Phase Equilib. Diffus., 2017, 38: 733

[58] Liu X J, Huang L S, Jiang H X, et al. Experimental investigation of the phase equilibria in the Co-V-Sn ternary system [J]. J. Phase Equilib. Diffus., 2017, 38: 723

[59] Liu X J, Yang S Y, Xiong H P, et al. Experimental investigation of phase equilibria in the Co-Ni-Zr ternary system [J]. Int. J. Mater. Res., 2016, 107: 887

[60] Ruan J J, Wang C P, Yang S Y, et al. Experimental investigations of microstructures and phase equilibria in the Co-V-Ta ternary system [J]. J. Alloys Compd., 2016, 664: 141

[61] Wang C P, Zhao C C, Lu Y, et al. Experimental observation of magnetically induced phase separation and thermodynamic assessment in the Co-V binary system [J]. Mater. Chem. Phys. Lett., 2015, 162A: 555

[62] Wang C P, Yang S, Yang S Y, et al. Experimental investigation of the phase Equilibria in the Co-Nb-V ternary system [J]. J. Phase Equilib. Diffus., 2015, 36: 592

[63] Ruan J J, Wang C P, Zhao C C, et al. Experimental investigation of phase equilibria and microstructure in the Co-Ti-V ternary system [J]. Intermetallics, 2014, 49: 121

[64] Wang C P, Zhao C C, Lin Z, et al. Experimental determination and thermodynamic calculation of the phase equilibria in the Co-Mn-Ta system [J]. Int. J. Mater. Res., 2014, 105: 1179

[65] Zhao C C, Yang S Y, Liu X J, et al. Experimental determination of the phase equilibria in the Co-Cr-Ta ternary system [J]. J. Alloys Compd., 2014, 608: 118

[66] Liu X J, Yu Y, Lu Y, et al. Interdiffusion and atomic mobilities in fcc Co-Ga and Co-V Alloys [J]. J. Phase Equilib. Diffus., 2018, 39: 2

[67] Sundman B, Jansson B, Andersson J O. The thermo-calc databank system [J]. Calphad, 1985, 9: 153

[68] Gómez-Acebo T, Navarcorena B, Castro F. Interdiffusion in multiphase, Al-Co-Cr-Ni-Ti diffusion couples [J]. J. Phase Equilib. Diffus., 2004, 25: 237

[69] Chen J, Liu Y J, Sheng G, et al. Atomic mobilities, interdiffusivities and their related diffusional behaviors in fcc Co-Cr-Ni alloys [J]. J. Alloys Compd., 2015, 621: 428

[70] Chen W M, Zhang L J, Li W, et al. Experimental measurements of the interdiffusivities in fcc Co-rich Co-Ti, Co-W and Co-Ti-W systems [J]. Int. J. Refract. Met. Hard. Mater., 2018, 71: 153

[71] Cui Y W, Jiang M, Ohnuma I, et al. Computational study of atomic mobility in Co-Fe-Ni ternary fcc alloys [J]. J. Phase Equilib. Diffus., 2008, 29: 312

[72] Moon K W, Campbell C E, Williams M E, et al. Diffusion in fcc Co-rich Co-Al-W alloys at 900 and 1000 ℃ [J]. J. Phase Equilib. Diffus., 2016, 37: 402

[73] Wang J F, Wang Y, Zhu N Q, et al. Experimental and computational study of interdiffusion for fcc Ni-Co-W alloys [J]. J. Phase Equilib. Diffus., 2017, 38: 37

[74] Wang Y, Lu X G. Interdiffusion and diffusion mobility for fcc Ni-Co-Mo alloys [J]. J. Phase Equilib. Diffus., 2017, 38: 656

[75] Wang Y, Zhu N Q, Wang H, et al. Interdiffusion and diffusion mobility for fcc Ni-Co-Al alloys [J]. Metall. Mater. Trans., 2017, 48A: 943

[76] Zhang W B, Liu D D, Zhang L J, et al. Experimental investigation and computational study of atomic mobility in fcc ternary Co-Cr-W alloys [J]. Calphad, 2014, 45: 118

[77] Zhou Z, Liu Y J. Atomic mobilities and diffusivities in fcc Co-Cr-Ti alloys [J]. J. Phase Equilib. Diffus., 2016, 37: 155

[78] Moelans N, Blanpain B, Wollants P. An introduction to phase-field modeling of microstructure evolution [J]. Calphad, 2008, 32: 268

[79] Kundin J, Mushongera L, Emmerich H. Phase-field modeling of microstructure formation during rapid solidification in Inconel 718 superalloy [J]. Acta Mater., 2015, 95: 343

[80] Lopez-Galilea I, Huth S, Fries S G, et al. Microsegregation and secondary phase formation during directional solidification of the single-crystal Ni-based superalloy LEK94 [J]. Metall. Mater. Trans., 2012, 43A: 5153

[81] Ta N, Zhang L J, Du Y. Design of the precipitation process for Ni-Al alloys with optimal mechanical properties: A phase-field study [J]. Metall. Mater. Trans., 2014, 45A: 1787

[82] Zhu J Z, Wang T, Ardell A J, et al. Three-dimensional phase-field simulations of coarsening kinetics of γ′ particles in binary Ni-Al alloys [J]. Acta Mater., 2004, 52: 2837

[83] Wu X C, Li Y S, Liu W, et al. Dynamics evolution of γ′ precipitates size and composition interface between γ/γ′ phases in Ni-Al alloy at different aging temperatures [J]. Rare Met., 2016, 1

[84] Takahashi A, Kobayashi Y, Kikuchi M. Phase field simulation of rafting behavior of γ' phase in nickel base superalloy [J]. Adv. Mater. Res., 2008, 33-37: 471

[85] Mushongera L T, Fleck M, Kundin J, et al. Effect of Re on directional γ′-coarsening in commercial single crystal Ni-base superalloys: A phase field study [J]. Acta Mater., 2015, 93: 60

[86] Yang M, Zhang J, Wei H, et al. Study of γ′ rafting under different stress states—A phase-field simulation considering viscoplasticity [J]. J. Alloys Compd., 2018, 769: 453

[87] Gao Y P, Ding H, Jin X J. γ' precipitation during ageing of a CoAlW alloy by phase field simulation [J]. J. Jilin Univ. (Eng. Technol. Ed.), 2011, 41: 84

[87] (高一鹏, 丁 洪, 金学军. CoAlW合金时效过程中γ'相析出的相场模拟 [J]. 吉林大学学报(工学版), 2011, 41: 84)

[88] Koyama T. Simulation of microstructural evolution based on the phase-field method and its applications to material development [J]. J. Jpn. Inst. Met., 2009, 73: 891

[88] (小山敏幸. フェーズフィールド法に基づく 組織形成シミュレーションとその材料開発への応用 [J]. 日本金属学会誌, 2009, 73: 891)

[89] Jokisaari A M, Naghavi S S, Wolverton C, et al. Predicting the morphologies of γ' precipitates in cobalt-based superalloys [J]. Acta Mater., 2017, 141: 273

[90] Shang S L, Zhou B C, Wang W Y, et al. A comprehensive first-principles study of pure elements: Vacancy formation and migration energies and self-diffusion coefficients [J]. Acta Mater., 2016, 109: 128

[91] Han J J, Wang C P, Liu X J. A modified model to predict self-diffusion coefficients in metastable fcc, bcc and hcp structures [J]. J. Phase Equilib. Diffus., 2013, 34: 17

[92] Neumann G. A model for the calculation of monovacancy and divacancy contributions to the impurity diffusion in noble metals [J]. Phys. Status Solidi, 1987, 144B: 329

[93] Mantina M, Wang Y, Chen L Q, et al. First principles impurity diffusion coefficients [J]. Acta Mater., 2009, 57: 4102

[94] Hargather C Z, Shang S L, Liu Z K. A comprehensive first-principles study of solute elements in dilute Ni alloys: Diffusion coefficients and their implications to tailor creep rate [J]. Acta Mater., 2018, 157: 126

[95] Zeng Y Z, Bai K W. High-throughput prediction of activation energy for impurity diffusion in fcc metals of Group I and VIII [J]. J. Alloys Compd., 2015, 624: 201

[96] Wu H, Lorenson A, Anderson B, et al. Robust FCC solute diffusion predictions from ab-initio machine learning methods [J]. Comp. Mater. Sci., 2017, 134: 160

[97] Wang C P, Qin S Y, Lu Y, et al. Interdiffusion and atomic mobilities in fcc Co-Cr-Mo alloys [J]. J. Phase Equilib. Diffus., 2018, 39: 437

[98] Yang Y L, Shi Z, Luo Y S, et al. Interdiffusion and atomic mobility studies in Ni-rich fcc Ni-Co-Al alloys [J]. J. Phase Equilib. Diffus., 2016, 37: 269

[99] Shi L, Yu J J, Cui C Y, et al. Effect of Ta additions on microstructure and mechanical properties of a single-crystal Co-Al-W-base alloy [J]. Mater. Lett., 2015, 149: 58

[100] Morinaga M, Yukawa N, Adachi H, et al. New PHACOMP and its application to alloy design [J]. Superalloys, 1984, 1984: 523

[101] Fischer C C, Tibbetts K J, Morgan D, et al. Predicting crystal structure by merging data mining with quantum mechanics [J]. Nat. Mater., 2006, 5: 641

[102] Ren F, Ward L, Williams T, et al. Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments [J]. Sci. Adv., 2018, 4: eaaq1566

[103] Nosengo N. Can artificial intelligence create the next wonder material? [J]. Nature, 2016, 533: 22

[104] Raccuglia P, Elbert K C, Adler P D F, et al. Machine-learning-assisted materials discovery using failed experiments [J]. Nature, 2016, 533: 73

[105] Guo J T, Hou J S, Zhou L Z, et al. Prediction and improvement of mechanical properties of corrosion resistant superalloy K44 with adjusting minor additions C, B and Hf [J]. Mater. Trans., 2006, 47: 198

[106] Yu J X, Guo S, Chen Y C, et al. A two-stage predicting model for γ′ solvus temperature of L12-strengthened Co-base superalloys based on machine learning [J]. Intermetallics, 2019, 110: 106466

[107] Burges C J C. A tutorial on support vector machines for pattern recognition [J]. Data Min. Knowl. Dis., 1998, 2: 121

[108] Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection [J]. IEEE Trans. Pattern Anal. Mach. Intell., 1997, 19: 711

[109] Breiman L. Random forests [J]. Mach. Learn., 2001, 45: 5