1.引言

工业管道作为化学工业的“血管”，在化工生产中扮演重要的角色。大多数工业管道都是在施工现场进行焊接和安装，由于施工现场条件比较复杂，施工的质量容易受到影响；另外，在定期检验过程中，经常会遇到现场工业管道与设计图纸不符的情况。以上的种种原因都可能导致压力管道在运行过程中出现事故，导致人员和财产损失。如何能够保证工业管道运行安全，一直以来都是广大学者研究的重点方向。

随着科学技术的进步，越来越多的学者使用有限元分析软件对工业管道进行应力分析和强度评定，有限元分析方法也得到了学界的认可。淡勇等采用有限元方法对超高压管道进行应力分析和强度评定，并对计算结果进行分解和应力分类。白芳等利用模拟与实验相结合的方法对X80钢多层焊道的残余应力进行研究。柏慧等研究了热辐射对加氢反应器热箱部位温度及应力分布的影响，考虑热辐射会使热箱部位的温度场分布更均匀，应力显著减小。许金沙等研究了搪玻璃层热膨胀系数、温差、厚度三个因素对搪玻璃层耐温差急变性能的影响，并通过试验研究对数值模拟结果进行了验证。吴新丽等采用Sysweld建立焊接模型，对经历不同热处理工艺的管板与环形支承板对接焊缝的焊接残余应力进行模拟分析，同时将模拟计算应力值与盲孔法测试应力值进行比较，并通过模拟试验验证其力学性能。霍玉峰等建立了钢渣罐三维瞬态热弹塑性仿真模型，对缓冷过程钢渣罐的温度场进行了分析，对罐体和纵横加劲肋等典型部位的应力和塑性应变也进行了分析。苏文献等利用有限元分析软件对复杂载荷作用下带夹套缩聚釜泄漏进行失效分析与改进设计。黄云等采用有限元方法研究单、双重裂纹的尺寸和位置变化对油气管道应力的影响，并拟合得出相应公式。张国威等基于热-结构耦合的干气压缩机出口输气管道进行应力分析，当管道温差过大时，外壁所受应力较大。伍颖等对管道上典型的平滑凹痕缺陷，根据管道的实际运行状况，建立了有限元模型，并得出应力随各参数的变化规律，采用非线性回归分析方法对计算结果进行了拟合。帅健等分析占压载荷作用下管道的应力与变形，管道在上覆土体和夯实地基的不均匀作用下发生局部弯曲和椭圆化变形。

从上文的文献中可以得出，国内外学者对于管道应力分析方面进行了大量的研究，但是大部分研究都是忽略温度下的单一和复杂载荷作用下的压力管道应力和强度分析，局限性比较大。本文研究了某化工企业中一条高温高压管道，建立了管道管件和焊缝的三维物理模型，利用有限元分析方法，研究了管道和焊缝在设计工况和使用工况下应力场和温度场随时间变化的情况，并基于分析设计标准进行应力评定，确定安全使用范围。

2. 有限元模型

2.1 物理模型和材料属性

该管道为某化工企业在用工业管道，在管道管件弯头与三通焊缝连接处发现焊缝未焊满情况，如图1（a）中红色框所示。从现场测量后得出，焊缝高度与管道表面相差10mm左右。管道整体设计压力为44.8Mpa，设计温度为260℃；工作压力为38Mpa，工作温度为110℃。三通管外径为241.3mm，内径为125.1mm；弯管外径为241.3mm，内径为140.9mm。管道焊缝焊接系数0.85。由于本文主要研究三通和弯管连接处焊缝的应力分布情况，因此只选取了管道的三通和弯管这一部分进行有限元分析。三通、弯管和焊缝的物理模型完全按照设计图纸的尺寸来建立，如图1（b）中所示。

三通和弯管材质为ASME标准的SA-182F11 CL2，焊缝材质保持与管件材质一致。管件材料的热膨胀系数、弹性模量、导热系数、泊松比和密度等特性参数参照ASME-SECTION Ⅱ PART-D中的材料特性进行选取。

图1 管道实物和三维物理模型

2.2单元选择和网格划分

在管道结构分析中有限元模型选择了8 节点六面体结构分析单元Solid185单元。Solid185 单元用于构造三维实体结构模型，该单元具有塑性、超弹性、应力刚化、蠕变、大变形和大应变等功能。对于管道温度场分析的有限元模型，选择8 节点的等参单元Solid 70单元。Solid 70单元可用于三维的稳态或瞬态热分析问题，并可以补偿由于恒定速度场质量输运带来的热流损失。管道物理模型的网格单元数为387 040，网格节点总数为413 987。对三通管和弯管连接的焊缝处进行网格加密处理，以确保满足计算精度要求。管道整体网格细节如图2所示。

图2 管道网格模型

2.3边界约束条件

管道应力分析模型边界条件如图3所示，弯管端面A施加全位移约束、管道内表面B施加垂直表面方向的内压力、三通管两个端面C和D分别施加垂直端面向外的拉力。三通端面上施加的压强可由Lame方程进行确定，Lame方程计算公式如下：

   （1）

式中：P为设计压力或工作压力，Mpa；K为端面处管外径与管内径之比；P2为三通管端面处受到的压力，Mpa。

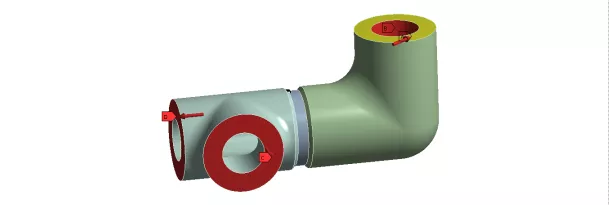
图3 边界条件

在设计工况和使用工况下管道应力分析模型边界条件具体设置如表1所示。

表2 温度分析边界条件管道温度场分析模型的内表面的温度在设计工况下设置为设计温度，在使用工况下设置为工作温度，由于管道外表面没有保温，根据环境条件设置自然对流换热系数。为了得到管道和焊缝应力场和温度场随时间变化的关系，则在非稳态条件下设置计算总时间为1000s，时间步长为50s。在设计工况和使用工况下管道温度模型边界条件具体设置如表2中所示。

表2 温度分析边界条件

3 .结果分析

3.1温度分布

图4中给出了使用工况下50s和1000s时刻管道温度分布情况。从图4（a）中可以看出管道内壁最高温度为110℃，管道外壁最低温度为34.2℃，管道内外温差75.8℃。最低温度出现在弯管内侧。从图4（b）中可得到在1000s时刻管道外壁最低温度为104.9℃，管道内外温差15.1℃。在1000s时刻管道整体温度分布较50s时刻更为均匀，管道内外壁温差降低60.7℃，最低温度由弯管内侧移至三通接口处。

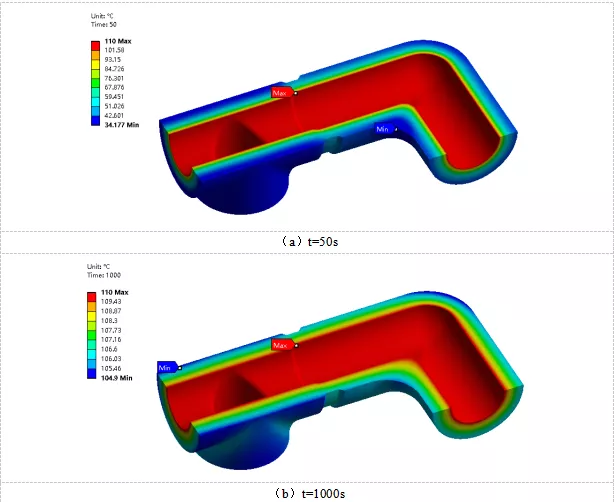
图4 使用工况温度分布

图5中同样给出了设计工况下50s和1000s时刻管道温度分布情况。从图5（a）中可以看出管道内壁最高温度为260℃，在50s时刻管道外壁最低温度为50.5℃，管道内外温差209.5℃。最低温度同样出现在弯管内侧。从图5（b）中可得到在1000s时刻管道外壁最低温度为245.8℃，管道内外温差14.2℃。在1000s时刻管道整体温度分布较50s时刻更为均匀，管道内外壁温差降低195.3℃，最低温度由弯管内侧移至三通接口处，与使用工况下相似。

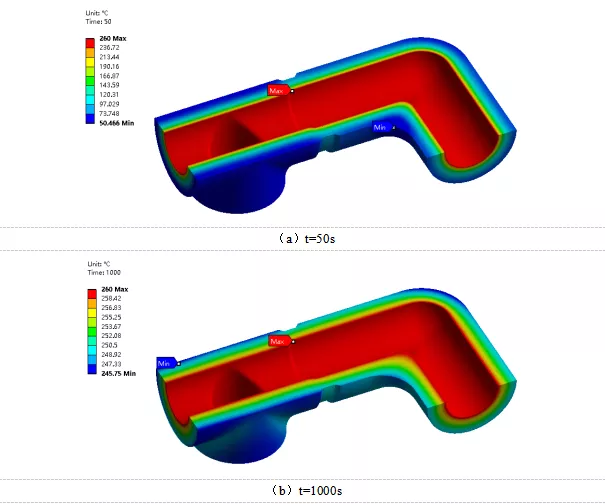
图5 设计工况温度分布

图6中给出了两种工况下管道各个时刻的最低温度随时间变化关系。从图中可以看出，随着时间的增加，管道温度不断升高。在使用工况下，300s之前升温速度较快，300s之后温度逐步平稳，700s之后温度基本不再变化，在1000s时刻温度达到104.9℃，此时管道温度已经达到平衡状态。在设计工况下，400s之前升温速度较快，400s至800s之间升温速度较慢，800s之后温度也基本不再变化，在1000s时刻温度达到245.8℃。

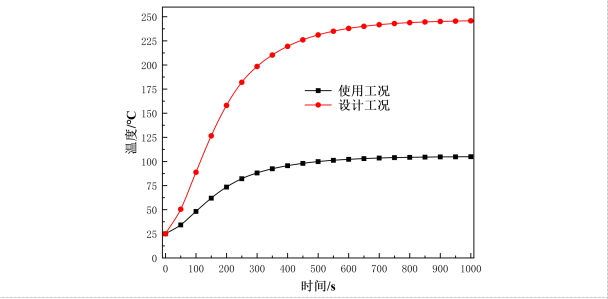
图6 两种工况下管道温度随时间的变化

3.2应力分布

图7中是管道在使用工况下50s和1000s时刻应力分布情况。从图7（a）中可以看出，在50s时刻，管道最大应力为430.1Mpa，最大应力点出现在弯管外侧表面处；焊缝处应力水平较焊缝两侧有明显的升高，焊缝处最大应力为305Mpa，最大应力点出现在焊缝外表面处。从图7（b）中可以得到，在1000s时刻，管道最大应力为380.8Mpa，最大应力点出现在弯管内侧表面处；焊缝处最大应力为210.8Mpa，最大应力点出现在焊缝外表面处。对比图7（a）和（b）发现，随着时间增加管道最大应力降低了49.3Mpa，焊缝处最大应力降低了94.2Mpa，管道最大应力点由弯管处外表面转移到内表面，焊缝最大应力点基本没有变化。

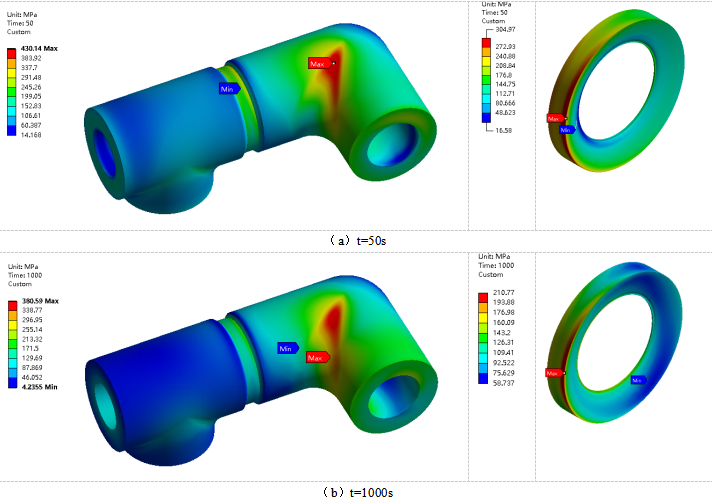
图7 使用工况应力分布

图8中是管道在设计工况下50s和1000s时刻应力分布情况。从图8（a）中可以看出，在50s时刻，管道最大应力为684.3Mpa，最大应力点出现在弯管内侧表面处；焊缝处应力水平较焊缝两侧有明显的升高，焊缝处最大应力为529.8Mpa，最大应力点出现在焊缝外表面处。从图8（b）中可以得到，在1000s时刻，管道最大应力为454.2Mpa，最大应力点出现在弯管外侧表面处；焊缝处最大应力为259.2Mpa，最大应力点出现在焊缝外表面处。对比图8（a）和（b）发现，随着时间增加管道最大应力降低了230.1Mpa，焊缝处最大应力降低了270.6Mpa，管道最大应力点由弯管处内表面转移到外表面，焊缝最大应力点基本没有变化。

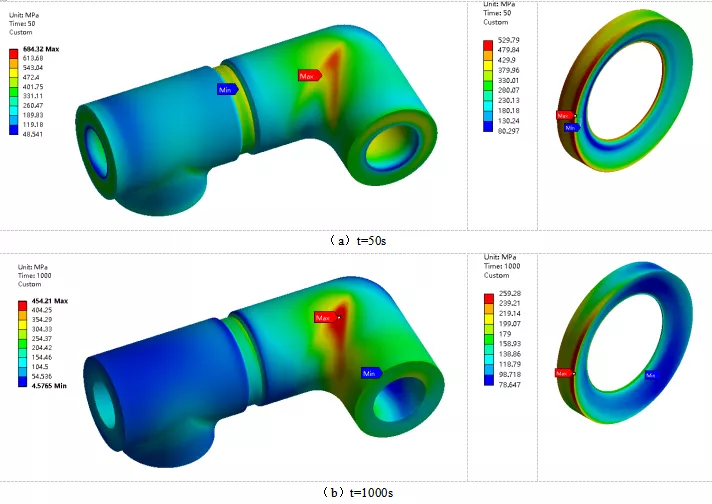
图8 设计工况应力分布

图9中给出了使用工况和设计工况下管道和焊缝最大应力随时间变化情况。图9（a）中是管道整体最大应力随时间变化情况，在两种工况下，管道最大应力都是随着时间增加而降低；在设计工况下，400s之前管道应力下降速率较大，400s之后管道应力下降速率较小，400s之后管道最大应力基本不发生变化；在使用工况下，300s之前管道应力下降速率较大，300s之后管道应力基本不再变化。图9（b）中是焊缝最大应力随时间变化情况，焊缝最大应力随着时间增加而降低；在设计工况下，500s之前焊缝应力下降速率较大，500s之后下降速率降低，500s之后焊缝最大应力基本不再变化；在使用工况下，300s之前焊缝应力下降速率较大，300s之后焊缝最大应力基本不发生变化。对照图6和图9发现，管道和焊缝的应力速率变化与管道温度速率变化有相互对应关系，温度变化速率大则应力变化速率也大，温度变化速率小则应力变化速率也小。

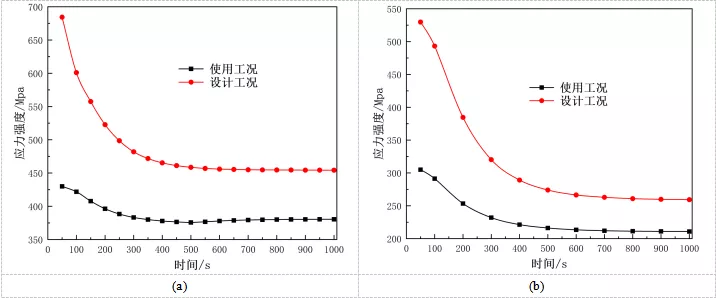
图9 两种工况下管道和焊缝最大应力随时间的变化情况

3.3强度评定

对两种工况下管道和焊缝应力集中处分别进行强度评定，评定依据为JB4732-1995（2005年确认）《钢制压力容器—分析设计标准》中关于弹性应力分析法的评估策略，利用线性化原理对应力集中处进行应力的分类评定。首先，通过最大应力节点，并沿着壁厚最短距离设置线性化路径；其次，三通和弯管连接处焊缝由于几何不连续，因此沿相交处所取截面结果所得的薄膜应力为一次局部薄膜应力PL，对应一次局部薄膜应力强度SⅡ；管道总体结构不连续区的弯曲应力应该归为二次应力的范畴，为了满足JB4732-1995（2005年确认）《钢制压力容器—分析设计标准》中对各应力强度依次逐级评定的要求，对薄膜应力加弯曲应力加二次应力按照SⅣ处理。应力评定强度结果如表3所示。

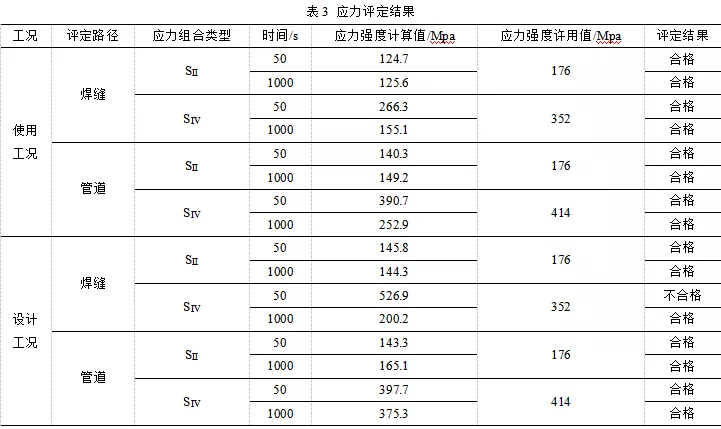
从表3中应力评定结果可以得出，在使用工况下管道管件和焊缝处均满足应力强度要求；在设计工况下管道管件满足应力强度要求，焊缝处在50s时刻应力评定为不合格，说明在设计工况下管道焊缝处初始升温过程中可能会出现开裂等失效情况，容易造成人员和财产损失。

4. 分析和讨论

通过对高压管道和焊缝进行温度分析、应力分析和强度评定，在得到分析结果后发现该管道在设计和使用中存在以问题：在管道设计工况下，对管道和焊缝进行应力分析得到应力分布情况，由于管道焊缝处有未焊满，导致在焊缝处存在应力集中现象；在对管道焊缝升温过程中进行线性化强度评定，发现在升温初始50s时焊缝处强度评定不合格，不满足强度要求。出现这种情况的原因为，在管道初始升温阶段管道内外温差较大，管道内二次应力水平较高，再加上高强度的机械载荷和局部应力集中现象，从而导致在焊缝等结构不连续处出现强度评定不合格。为了保证管道在设计工况下能够安全运行，应当在焊缝处进行补焊作业，使焊缝表面与管道表面平齐。当焊缝填满后，一方面焊缝强度得到提升，另一方面可以消除管道焊缝处结构不连续，降低应力集中影响。

5. 结论

以某化工企业一条高温高压管道和焊缝为研究对象，基于弹性分析策略评价了管道和焊缝处高应力区的应力强度，并分析了该管道和焊缝的温度分布和应力分布情况，得到以下结论：

在使用工况下，随着时间增加管道温度不断升高，1000s时管道温度为104.9℃，内外温差15.1℃；在设计工况下，随着时间增加管道温度不断升高，1000s时管道温度为245.8℃，内外温差14.2℃；管道内外温差随着时间增加而降低。

该管道在弯管和焊缝处存在应力集中现象，在使用工况下，弯管最大应力为430.1Mpa，焊缝最大应力为305Mpa；在设计工况下，弯管最大应力为684.3Mpa，焊缝最大应力为529.8Mpa；管道和焊缝最大应力随着时间增加逐渐减小。

对管道和焊缝升温过程中进行线性化强度评定，在使用工况下管道管件和焊缝处均满足应力强度要求；在设计工况下管道管件满足应力强度要求，管道焊缝处在50s时刻应力评定为不合格，不满足强度要求。

为了保证管道在设计工况下能够安全运行，应当在焊缝处进行补焊作业，使焊缝表面与管道表面平齐。