通常情况下，金属材料是由大量的晶粒组成的多晶体。当多晶体的晶粒取向相对于材料宏观的某一参考面（或方向）集中分布在某一个或某些取向附近的时候，我们称这种现象为择优取向（Preferred orientation），而织构就是多晶体的择优取向。从广义来看，多晶体中晶粒取向偏离随机分布的现象都可以称之为织构。

在金属材料中，织构现象的存在具有普遍性。外界的温度场、电磁场、应变场以及晶体内部的各向异性等因素，都可以引起织构，比如形变过程中的晶粒择优取向是晶体固定的滑移/孪生面和拉伸时产生力矩作用的结果。工业上材料常见有铸造织构、形变织构、再结晶织构和相变织构等，其中对形变织构和再结晶织构研究得较多。

【织构的表示方法】

（1）晶体取向的描述及织构的常见类型

所谓晶体取向就是指晶体的三个晶轴（如[100]、[010]、[001]轴）在给定参考坐标系（如轧板中的轧向RD、侧向TD和法向ND）内的相对方位。在实际描述晶体取向时，因形变条件不同而设定不同的参考系，比如对于最常见的轧制变形，通常设定参考系的三个轴为轧制方向（RD）、轧制面的法向（ND）以及轧板的横向也就是在轧面上与轧向垂直的方向（TD），假设一个取向表示为(110)[1-12]，就说明此时晶胞的(110)面平行于轧面，[1-12]方向平行于轧向。

织构的类型主要取决于金属的本质及加工方式等，其中有轧制织构、拉拔织构等。轧制织构是在轧制形变时出现的织构，它的特点是各个晶粒的某一晶面{hkl}平行于轧制面，某一方向<uvw>平行于轧制方向，这样的轧制织构通常表示为{hkl}<uvw>。而单向拉伸和拉拔变形会使多晶体晶粒的某个方向平行于拉伸或拉拔方向，这样形成的织构称为丝织构，也叫做纤维织构，以平行于拉伸或拉拔方向的晶向<uvw>表示。

（2）极图

极图是表示被测材料中各晶粒的某一选定晶面{hkl}在包含样品坐标系方向的极射赤面投影图上的取向分布图形，这个图形就称作{hkl}极图。图1就是Cu-30%Zn合金经96%轧制后的{111}极图，经过取向分析就可以得知，材料中的织构组分主要是{110}<1-12>织构，也叫做黄铜织构。

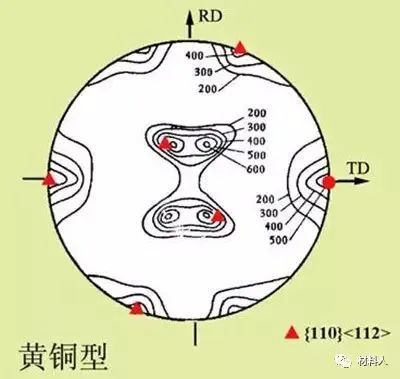
图1 Cu-30%Zn合金经96%轧制后的{111}极图

（3）反极图

和极图相反，反极图是描述多晶体材料中平行于材料的某一外观特征方向在晶体坐标系中的空间分布的图形。参考坐标系的三个轴一般取晶体的三个晶轴或低指数的晶向，对于立方晶系，由于具有24次对称性，所以只选择[001]-[101]-[111]的部分进行描述。反极图一般用于描述丝织构，图2表示的就是一种热轧低碳钢平行于法向ND方向的反极图，可以看出，材料中存在<111>和<100>丝织构。

图2 热轧低碳钢的ND反极图

（4）取向分布函数

极图和反极图是用二维图形来描述三维空间的取向分布，它们都有局限性。而采用空间取向g(φ1,Φ,φ2)的分布密度f(g)则可以表达整个空间的取向分布，这称为空间取向分布函数（ODF）。ODF是根据极图的极密度分布计算出来的三维图形，由于用立体图表示不方便，一般用固定φ2的一组截面来表示，图3就表示工业纯铝经95%形变量冷轧后的ODF图。

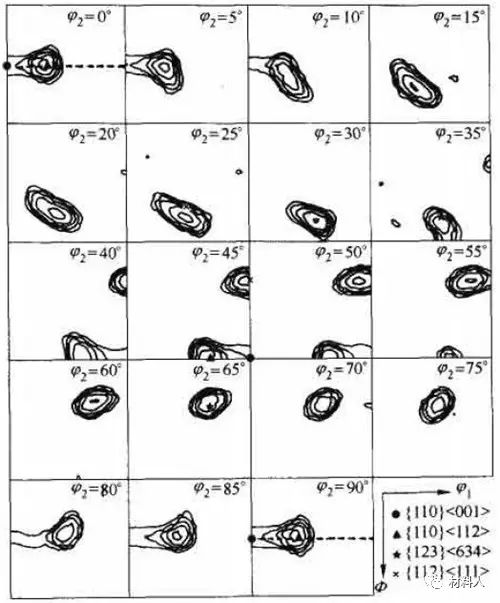
图3 工业纯铝经95%形变量冷轧后的ODF图

【织构对性能的影响】

大量的实验结果表明，材料的性能20%-50%受织构影响，织构会影响弹性模量、泊松比、强度、韧性、塑性、磁性、电导、线膨胀系数等多种材料的力学性能和物理性能，下面就介绍几个研究织构对材料性能影响的示例。

人们研究最多的就是织构对材料静态力学性能的影响，图4表示的是一种商业镁合金在搅拌摩擦焊工艺的影响下产生强烈的基面织构，从而材料的不同部位不同方向的拉伸性能就表现出差异。比如以经过摩擦焊（FSP）工艺处理的样品为例，材料在样品宽度方向也就是横向（TD）的拉伸强度要显著高于加工方向（PD），表现出显著的各向异性。

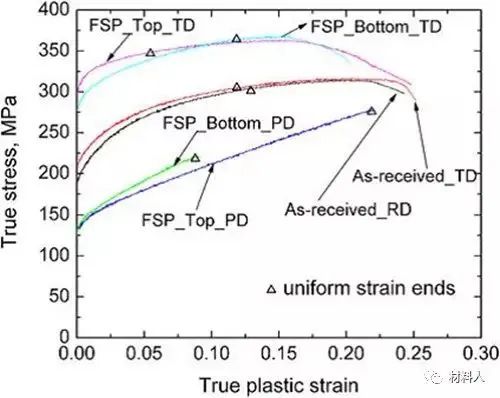
图4 AZ31镁合金原始轧态及搅拌摩擦焊后不同样品取向的拉伸性能

织构还会对材料的弹性性能产生影响，图5表示的是织构对一种金薄膜的弹性模量的影响，图中的三个图分别表示的是单晶金在晶体坐标系下、无织构的金薄膜在样品坐标系下以及含有丝织构的金薄膜在样品坐标系下的弹性模量参数曲面，可以看出，织构使得材料的弹性模量出现各向异性，沿着材料不同方向的弹性模量表现出显著差异，材料沿S3方向的弹性模量为118 GPa，要高于S1和S2方向弹性模量的89.7 GPa，而弹性模量的最小值是沿着偏离S3方向约40度的方向，模量值仅为60 GPa。

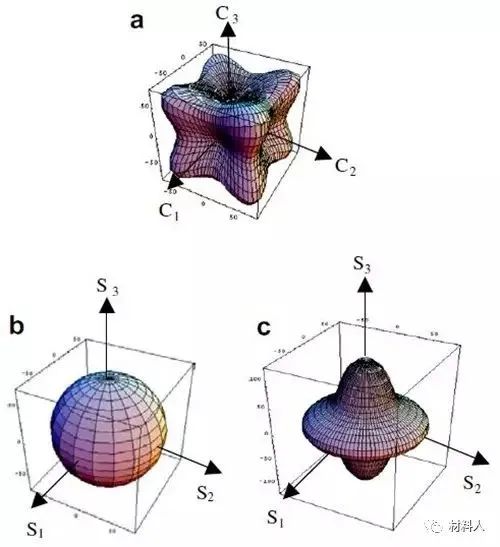
图5 织构对一种金薄膜弹性模量的影响

腐蚀行为也受到织构的影响，图6表示的是商业纯钛在经历不同次数等通道转角挤压变形后的阻抗谱Nyquist图，经历变形的次数不同，材料内部的微观组织以及织构成分也就不同，可以看出，材料在初始状态未经历变形（0 pass）时候的抗腐蚀性能较好。

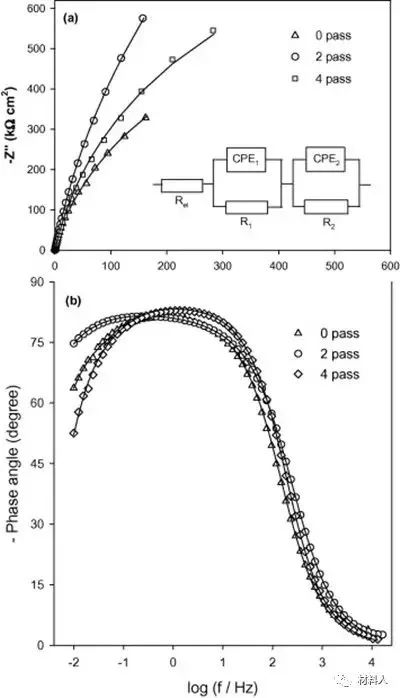
图6 等通道转角挤压对商业纯钛阻抗谱Nyquist图的影响

材料在动态循环载荷下的疲劳行为同样受到织构的影响，图7表示的是一种镁合金在经过挤压变形后，不同取向样品的低周疲劳行为就会不同。可以看出，在总应变幅相同的情况下，材料沿RD方向的疲劳寿命整体上要优于沿ND方向的疲劳寿命。

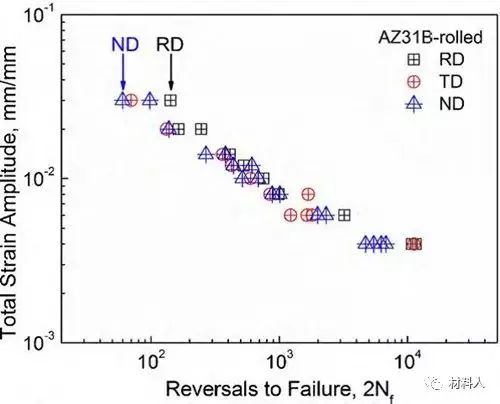
图7 织构对材料低周疲劳行为的影响

【小结】

综上所述，织构的存在在金属材料中具有普遍性。织构的本质就是许许多多的晶粒没有按照随机取向分布，这就自然会导致材料的性能出现各向异性。人们研究织构对材料性能的影响，目的就是为了能够更好的利用材料中的织构，从而来调控材料的相关性能。