腐蚀学科目前尚处于实验学科范畴，腐蚀理论仅起说明和解释作用，大量问题靠实验解决，基于实验数据的解析来取得规律、建立腐蚀预测模型是腐蚀计量学的重要任务。

    腐蚀现象起源材料表面微电池作用，含微观体系固有的随机特性，即：在完全相同条件也不一定得到相同结果。腐蚀数据解析需要有重复（平行）数据，依据数据信息量的完整程度，选择合理的解析方法是取得成功的关键。本文探讨其一般规律。

    1、腐蚀数据波动性和分布特性函数

    1.1  二类腐蚀数据

    有二类腐蚀数据。一类在本质上属于大量随机量的统计结果，如腐蚀失重、腐蚀电位、电偶电流等。它们的波动性主要来自测量误差，属于正态分布。这类数据用以平均值为中心的置信范围表示，可用常规解析分析和误差理论来处理。传统腐蚀研究主要针对这类数据。

    另一类数据波动性来自腐蚀现象自身随机性，服从物理学的测不准定律。由于来源不同，其随机波动的分布特征差别很大，但都不属正态分布。如，材料表面点蚀发生数量常属泊松分布、海水中钢的点蚀及缝隙腐蚀诱导期属指数分布、SCC破裂寿命属对数分布等等。它们平均值没有确切意义，也不能按常规误差理论处理，需要具体问题具体分析。

    1.2正态分布数据

    由大量、分散独立因素造成的随机体系往往服从正态分析。如以测量误差为主的腐蚀数据。这类数据的二种基本特征参数一是真值（期望值），可近似用多次测量平均值代替；二是波动指标，如数据精度、标准偏差、方差等等。其平均值在某些情况下可按确定值处理，但在数据比较、相关分析等方面还须考虑其波动性。例如，按配对对比试验或者随机对比试验获得的腐蚀数据需要根据其t值检验来判断两者是否存在差异。又例如，两个随机量之间的相关分析须考虑拟合公式置信度并进行误差分析等等。详细方法可参见相关书籍。

    1.3非正态分布的数据

    非正态腐蚀数据的处理要复杂得多，一般需首先确定其分布特性，再根据相应分布函数确定其特征参数。其参数数量可能超过二种。判断有限次数数据的随机分布类型有许多方法，如：χ2适度检验、K.S检验、线性无偏估计法、最大似然估计法，大多涉及复杂运算。有一种简便直观方法称为概率纸检验法。其原理是通过设置标准化变量，使分布函数转化为线性形式，然后在以标准化变量为坐标的纸（概率纸）上作图，如数据呈线性则表示符合这种分布，并估计其特征参数值。下表为几种常见腐蚀数据分布的标准化变量形式以及分布参数估计方法。

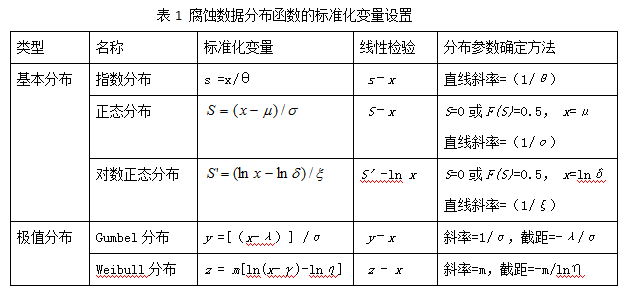
    这种方法也为非正态随机数提供了简便解析方法。但切记非正态随机数的平均值是没有意义的，两个随机量的比较需要采用更复杂方法处理，如：概率密度函数联合积分法或强度与应力差的概率密度函数积分法。

    2、依据数据信息完整程度选择解析方法

    2.1 信息完整体系采用分布函数方法解析

    全部波动特性已知的腐蚀数据称为信息完整体系，可其相应分布函数和特征参数来处理并描述其规律。此时先要区分正态分布和非正态分布，两类数据的解析方法不同，后者往往要复杂得多。

    2.2 特定部分信息已知的体系

    得到信息完整体系需做大量重复（平行）试验，有时很难做到。取特定的部分信息进行解析是一种好的途径。成熟的是极值分析，即根据波动的极大值或极小值信息进行分析。尽管信息完整的腐蚀数据分布类型很多，最常见有正态分布、泊松分布、指数分布、对数正态分布四大类，但无论基本分布形式如何，其极值分布类型要简单得多，常见的是：第一类的最大值分布（Gumbel分布）和第三类的最小值分布（Weibull分布）。前者有二个特征参数λ（位置参数）和α（尺度参数）；后者有三个特征参数γ（位置参数）、η（尺度参数）和m（形状参数）。

    极值分析方法较复杂，可借助计算机编程，或采用表1的变量转换及概率纸方法计算。

    2.3 貧信息体系和模式识别方法

    全部或局部特征信息未知的数据属于信息学“灰箱”或“黑箱”，统称貧信息体系。精确数学方法对这类体系无能为力。模式识别（PR, Patten Recognition）是化学计量学里为这类体系提供的常用方法。目前计算机模式识别能做到的只限于对客观事物按其特征进行分类，离“理解”还有相当距离，模式识别不只是对人能力的简单替代，许多情况下还可完成人能力无法胜任的工作，如对高维信息的处理。用模式识别解析时需要以下基本条件：

    （1）有合格数据，如研究环境-腐蚀性的数据必须同时包含腐蚀性指标和环境腐蚀因素等全面的数据；

    （2）确定描述模式的元素（关键因素），它们必须是可以被计算机接纳和处理的；

    （3）要有足够量的数据和数据信息量，足以反映腐蚀数据模式的主要特征；

    （4）选择好方法，目前主要用统计模式识别（Statistical PR）来处理数据；用句法模式识别（Syntactic PR）来处理图形。

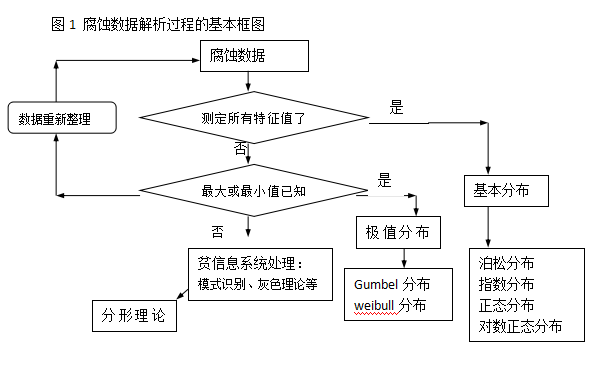
    统计模式识别有很多种，如：主分量分析、聚类分析等。从广义角度说，灰色理论、神经网络等都可归入此类方法。模式识别的解析能力往往超过常规数理统计方法，原因之一是采取以含模糊界线的分类来替代准确的数值计算。上述过程可归纳成下面框图：

    模式识别方法对腐蚀数据处理的成功应用实例很多，如主分量分析在建立土壤腐蚀性类别和其理化参数之间数学模型、聚类分析在现场土壤失重试验中的埋点设计、区域土壤腐蚀性预测模型的建立等。更多应用实例还可参见其它资料。

    3、更多新解析方法的尝试

    3.1分形方法

    分形方法和混沌理论被比作继经典力学、相对论及量子力学之后的物理学第三个里程碑。之前的物理学可解释上至宇宙天体，下至微观粒子，几乎尽善尽美，但对于位于其间尺度的大量自然现象，尤其是那些不可逆的复杂随机现象，如：天气预报、海岸线长度测量等往往无能为力。分形方法在腐蚀数据解析上的成功应用反过来证明腐蚀现象具有某些混沌或分形特征。这种新解析方法优点至少表现在以下几个方面。

    （1）能够处理包括腐蚀图像在内的更多数据类型；

    （2）能够揭示腐蚀现象的某些本质或机理问题。

    以下用我们的部分工作成果说明。

    3.1.1 揭示腐蚀图像分维和表面坑深分布的关联

    分形体系几何特征之一是具有分数维，可通过数学方法计算出任何复杂腐蚀图像的分维。另一方面，腐蚀表面坑深和坑数量之间服从分形体系的幂函数关系，即：坑深越大，数量越少，两者在双对数坐标成线性，其斜率称为坑深分布分维。研究发现，图像分维和坑深分布分维有很好一致性。这为用简便的图像分维计算替代费时费力的坑深测量提供了途径。

    3.1.2 建立腐蚀分形动力学模型

    分形泛指在形体、功能或信息等方面具有自相似性的体系，分形建模就是寻找复杂体系内部的潜在规则，然后通过不断重复或复制来模拟整体的规律。我们假设存在三种不同腐蚀发生概率的表面形态，即：未腐蚀表面、已腐蚀表面和受腐蚀影响表面，采用单体凝聚Eden建立腐蚀发展的分形动力学模型。这种模型可以解释表面蚀点数量发展服从泊松分布、累计腐蚀量和时间之间服从幂函数等等一系列已知的腐蚀规律，并用来研究小试片的腐蚀边界效应。

    3.2大数据应用

    大数据分析是一种全新解析腐蚀数据的方法。大数据泛指数量之多和来源之广。例如，我们曾以塔里木现场埋片平行数据为基础，发现平均值和其标准偏差之间存在幂函数关系。这个规律后来也被分形动力学模型证实，揭示了腐蚀现象的分形特性。此外，通过大数据散布图还可获得更多信息。如某海上平台生产管线穿孔记录含时间，地点以及当时管内介质温度、压力、含水量、流速等参数，收集连续多年的数据，可估测其临界流速及历年的变化。发现超过临界流速、且管输介质含水量超过80%的管线，其寿命均不足2年，而含水量低于30%的管线寿命无一例外超过10年 。同样方法也曾用于大量数据研究埋地管线实测保护电位（未扣IR降）和实际保护效果的关系。

    综上所述，腐蚀数据解析需考虑被研究对象本质、数据完整程度及新方法的应用。这个领域尚有大量待研究课题，是大有作为的。

更多关于材料方面、材料腐蚀控制、材料科普等方面的国内外最新动态，我们网站会不断更新。希望大家一直关注中国腐蚀与防护网http://www.ecorr.org

责任编辑：王元

《中国腐蚀与防护网电子期刊》征订启事

投稿联系：编辑部

电话：010-62313558-806

邮箱：fsfhzy666@163.com

中国腐蚀与防护网官方 QQ群：140808414