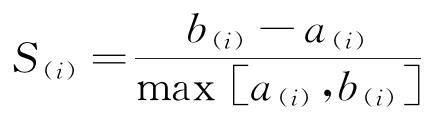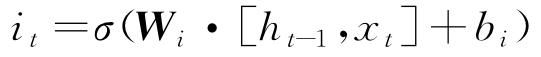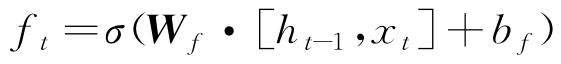管道运输是我国能源运输的主要形式之一,我国的运输管网体量十分庞大,截至2020年底,我国原油和成品油管网里程已超6万km,天然气管道总里程约11万km。我国油气管网覆盖面积大,且60%以上管道的运行时间超过20 a,由管道腐蚀泄漏引发的安全事故时有发生[1-3]。2013年发生在山东青岛的“11.22”事故导致62人死亡、136人受伤数,直接经济损失共计7.5亿元[4];2021年6月13日,湖北十堰市发生了一起燃气爆炸事故,导致了26人死亡、138人受伤[5]。以上事故原因均为管道腐蚀,为确保管道安全运行,需要定期对老旧管道进行监检测,确定其是否安全,并根据管道所处腐蚀阶段决定是否更换管道。
声发射检测是一种可以实时监测管道完整性的较为有效的方法。QIU等[6]建立了声发射典型参数腐蚀行为的定量表征公式,为应用声发射技术监测低碳钢的腐蚀提供了依据;SEGHIER等[7]提出的基于混合人工智能(SVR-GA、SVR-PSO和SVR-FFA)模型在预测油气管道最大点蚀深度时具有较高的适应性和准确性;SHEIKH等[8]针对加速腐蚀试验声发射信号提出的RBF-NN模型可以准确预测腐蚀程度;BHASKARAN等[9]利用K均值(K-means)聚类算法识别管道输油过程中发生的异常压力升降,再根据时间序列线性回归进一步估计管道系统因裂缝和堵塞引起的风险发生率。
长短期记忆(LSTM)神经网络在自然语言处理、语音识别等时序数据储量方面获得了巨大的成功[10]。但是国内运用LSTM神经网络预测管道腐蚀方面的研究较少,相关技术还不够成熟。基于此,作者提出一种基于K-means聚类算法和LSTM神经网络的管道腐蚀阶段预测模型(以下称本模型),以期实现管道腐蚀阶段的准确预测,为管道腐蚀检修提供有利的参考依据。
1. 原理与模型建立
1.1 K-means聚类算法
聚类分析的算法有很多,其中K-means算法应用范围较广,且具有计算复杂程度低、收敛速度快的优点。由于本次声发射检测得到的腐蚀数据量非常大,作者选取K-means算法对试验数据进行分类分析,以采集到的腐蚀信号为模型的输入项,并根据其特征规律将信号分成几个阶段。K-means算法核心思想是将距离相近的样本划分为一簇,使簇内距离尽量小,簇间距离尽量大,共划分出k个簇[11]。
如何确定簇数k是个非常重要的问题。K-means算法中相关指标有许多,此次选用轮廓系数S(i)来确定簇数。轮廓系数的计算公式见式(1)[12]。
|
|
(1) |
式中:a(i)反映了簇内的密集性,b(i)体现了簇间的分散性。最后,对所有点的轮廓系数求平均值,得到最终的平均轮廓系数。轮廓系数越接近1,表明簇内样本的平均距离越小,簇间的最短距离越大,聚类效果越理想。最后,选取轮廓系数最接近于1的数字为簇数k值[13]。
1.2 LSTM神经网络原理
LSTM神经网络是循环神经网络(RNN)在结构上的一种改进,适合处理和预测时间序列中间隔和延迟相对较长的管道腐蚀信号[14]。
LSTM神经网络引进门控机制(输入门、输出门和遗忘门)控制信息传输途径。输入门it控制当前时刻的候选状态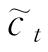 需要保留多少信息;输出门ot控制当前时刻的内部状态ct需要向外部状态ht输出多少信息[15];遗忘门ft控制前一时刻的内部状态ct-1需要忘记多少信息。三个门的计算方式分别为:
需要保留多少信息;输出门ot控制当前时刻的内部状态ct需要向外部状态ht输出多少信息[15];遗忘门ft控制前一时刻的内部状态ct-1需要忘记多少信息。三个门的计算方式分别为:
|
|
(2) |
|
|
(3) |
|
|
(4) |
式中:σ为sigmoid函数;xt为当前时刻的输入;ht-1为前一时刻的外部状态[16]。W表示权重系数矩阵;b表示偏置项。
图1为LSTM神经网络单元的结构[17],其计算过程如下:第一步,利用前一时刻的外部状态ht-1和当前时刻的输入xt,计算出三个门以及候选状态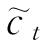 ;第二步,结合遗忘门ft和输人门it对记忆单元ct进行信息更新;第三步,结合输出门ot,将内部状态信息传给外部状态ht[18]。
;第二步,结合遗忘门ft和输人门it对记忆单元ct进行信息更新;第三步,结合输出门ot,将内部状态信息传给外部状态ht[18]。
1.3 模型构建
基于LSTM神经网络的管道腐蚀诊断流程如图2所示。首先,采集管道腐蚀声发射信号,利用K-means算法将信号按照轮廓系数分类;然后,将数据集分为70%的训练集和30%的测试集,在Python平台上建立LSTM神经网络模型,利用训练集数据对模型进行训练后,根据准确度和模型的稳定性进行参数优化;最后,将测试集数据输入训练好的模型中,输出腐蚀阶段结果,并通过测试集的准确率、均方根误差(RMSE)、平均绝对误差(MAE)、混淆矩阵等指标来评价模型的效果。
2. 管道点蚀检测试验
2.1 试验数据采集
采用油气管道设备中常用材料Q235钢为试样。试验前,用砂纸打磨试样,然后用丙酮清洗并烘干。腐蚀液为3.5%(质量分数)NaCl溶液,其pH为2。
在试样中间钻一个小圆坑,用于滴腐蚀液。为防止试样的非试验部分产生声发射信号,对其作封样处理。将封好的试样按照图3进行布置。传感器通过凡士林与圆坑两侧耦合固定,并通过电缆与声发射仪器的采集通道连接,实时监测来自圆坑内的腐蚀信号。试样与试验台之间衬有3 cm厚的泡沫板,以减少外界的振动干扰。
设置声发射仪门槛值为30 dB,每个波形记录2 048个样本点。在试样圆坑中滴入腐蚀液之后,开启声发射系统监测腐蚀信号。
2.2 结果与分析
2.2.1 波形的处理
声发射检测得到的信号一般都很复杂,采用简化波形特征参数分析信号可减小计算量。但分析简化的特征参数有一定的弊端,加上管道腐蚀信号复杂,使得简化特征参数的分析结果不能准确反映腐蚀过程中声发射信号的发生和变化情况。如果直接采用原始波形数据进行分析,计算量会很大,但是可以确保考虑到每个样本的特征。
作者对采集到的声发射波形进行尾切处理,再实现信号的聚类。其中,尾切是切除波形首尾不需要的信号,以保留波形中尽可能多的有用信息[19]。信号尾切处理后,共有78 500个信号,每个信号包含2 048个采样点。
图4为尾切后的波形图,可以看出整个腐蚀过程大致可以分成三个阶段。由于对数据进行了切除,所以起点不是从零开始的。刚开始一小段时间内的信号杂乱且弱,随着腐蚀试验的进行,波幅的整体趋势逐渐上升,达到峰值后,又逐步下降并趋于稳定。为了验证腐蚀阶段的分类问题,以下用K-means聚类算法对数据进行分类。
2.2.2 K-means聚类算法分析
在聚类分析前,利用轮廓系数法作为聚类标准判断合适的聚类簇数,基于Keras的Anaconda虚拟环境,绘制簇的个数从2到15时的轮廓系数图,如图5所示。轮廓系数越高,聚类效果越好。当k值取3时,轮廓系数最大,因此将数据聚为3类较为合理。
将数据导入OriginPro 2022软件进行K-means聚类。在统计中选择多变量分析,聚类簇数选择3,不指定初始聚类中心,并设置最大迭代次数为10次,最终得到聚类分析结果。
根据聚类分析结果,可以将腐蚀过程分为三个阶段:初始腐蚀期、加速腐蚀期、平稳腐蚀期。管道腐蚀声发射信号基本上都是突发型信号,其频谱图上频率都集中在一定的范围内。在不同腐蚀阶段,信号的波形特征明显不同。不同腐蚀阶段的部分试验数据见图6。图7是试验过程中AE信号的撞击数。
在初始腐蚀期,试样表面未发生明显腐蚀,产生的少量气泡吸附、分离和上浮,发生共振撞击,被传感器捕获到单个气泡破裂产生的声发射源信号,撞击次数小于2 000次。
在加速腐蚀期,试样表面钝化膜被破坏,腐蚀反应加速,试样表面许多气泡同时破裂。此外,腐蚀产物的脱落、摩擦和下沉过程导致波幅明显增加,最大撞击次数超过3 800次。
在稳定腐蚀期,对应点蚀进入稳定发展阶段,由于腐蚀产物的剥离和金属在坑下的进一步溶解,新的钝化膜逐渐形成。虽然该阶段的撞击次数有所减少,但仍高于腐蚀初期。
2.2.3 神经网络模型的建立与训练
作者在基于Keras的Anaconda环境中使用Python语言进行程序设计。
试验样本总共有78 500个信号。对数据进行归一化处理后,将70%的数据作为训练集、30%的数据作为测试集。
单层的LSTM网络难以学习到高维数据的时序性特征,而多层LSTM网络是将上一层的输出ht作为下一层的输入值xt,因此多层LSTM网络的学习能力更强[20]。
本模型采用的网络结构为输入层、LSTM层和全连接层,为了避免模型过拟合添加Dropout层。输出值个数设置为3,代表三种腐蚀阶段出现的概率。选用Adam作为优化器,学习率为0.001,损失函数设置为交叉熵损失函数(binary_crossentropy)搭配Softmax全连接层的激活函数使用。将批处理量设置为30,最大处理批次设置为128。
2.2.3.1 不设置隐藏层
图8为训练集和测试集的准确率和损失函数变化。从图8可以看到,整体准确率为97.54%,当训练集的迭代次数介于10~25时,准确率和损失函数曲线波动幅度略大,模型不稳定。
2.2.3.2 设置隐藏层
设置隐藏层神经元层数为10层,神经元数量为32,激活函数设置为ReLU函数。此时,准确率和损失函数变化曲线见图9。每一代的训练时间在2~4 s,整体准确率为98.99%,与不设置隐藏层时变化不大,但是模型整体拟合程度较高,训练集与测试集变化曲线基本持平,损失函数值在0%~0.2%,说明此模型的鲁棒性较高。
因此,适当增加层数的隐藏层能很好地解决准确率和损失函数曲线波动幅度大的问题,使得模型鲁棒性更好。
2.2.4 模型评价
选用RMSE、MAE和混淆矩阵对训练后模型的测试结果进行评价。模型的RMSE和MAE指数越接近于0,说明模型的鲁棒性越好。计算得到本模型的RMSE为0.039 6, MAE为0.007 4,混淆矩阵见图10。由图10可以看出,本模型仅有少量初始腐蚀期和平稳腐蚀期的信号混淆。
2.2.5 试验验证
为验证本模型的准确性,又做了两组平行试验。利用训练好的LSTM神经网络模型对平行试验采集到的声发射信号进行识别并验证。结果得到,准确率分别为96.44%和97.01%。此模型的准确率取三次试验准确率的平均值97.48%。
2.2.6 对比分析
用决策树、支持向量机、线性回归、朴素贝叶斯故障诊断方法进行分析,将以上方法的准确率与本模型的准确率进行了对比,结果如表1所示。
| 方法 | 准确率/% |
|---|---|
| 决策树 | 73.34 |
| 支持向量机 | 92.30 |
| 线性回归 | 80.31 |
| 朴素贝叶斯 | 89.20 |
| 本模型 | 97.48 |
从表1中可以看到,仅支持向量机模型和本模型的准确率高于90%,但本模型的准确率还是远超过包括支持向量机的其他分类器。对比分析结果证明,本模型能够较好地预测管道腐蚀阶段,具有良好的泛化能力和性能优势,并远远优于其他机器学习方法。
3. 结论
(1)基于K-means聚类算法和LSTM神经网络建立了油气管道腐蚀阶段的预测模型。
(2)LSTM神经网络模型可以直接对原始声发射信号进行训练与预测,有效地解决了管道腐蚀阶段诊断过程中复杂的数据预处理、特征选取等问题。
(3)适当增加隐藏层,对模型测试集曲线波动幅度和模型稳定性有较好的改善。
(4)与传统决策树、支持向量机、朴素贝叶斯等传统预测方法相比,本模型对管道腐蚀的预测准确率更高,为97.48%,并采用准确率、损失函数、RMSE等多种评价指标对模型进行评价,提高模型预测结果的可信度。
免责声明:本网站所转载的文字、图片与视频资料版权归原创作者所有,如果涉及侵权,请第一时间联系本网删除。

官方微信
《腐蚀与防护网电子期刊》征订启事
- 投稿联系:编辑部
- 电话:010-62316606
- 邮箱:fsfhzy666@163.com
- 腐蚀与防护网官方QQ群:140808414