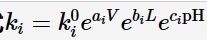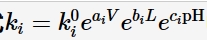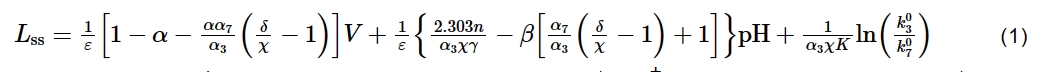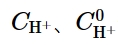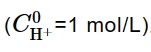304不锈钢具有优良的耐蚀性[1,2]而在工业中有广泛的应用。金属表面通常存在一层薄薄的 (通常厚度为几个纳米到几个微米) 的亚稳态腐蚀产物,使得金属能在相应的服役环境中稳定存在。304不锈钢的耐蚀性能已被广泛研究,同时,它也是很多模型测试钝化态的一种理想材料。很多研究[3~6]表明点缺陷模型 (PDM) 能很好地解释Fe-Cr合金的钝化状态,但是很少有研究对其基础的反应动力学参数进行分析。PDM能够通过实验分析验证其可靠性,并预测实际环境腐蚀进程[7~9]。此外,PDM还可以通过最优化拟合分析电化学阻抗数据[10,11]。本研究利用PDM,研究304不锈钢在pH=1.4~13.5溶液中稳态钝化膜的生长,分析电化学阻抗谱和莫特-肖特基数据,并提取动力学参数用于预测304不锈钢在不同条件下的腐蚀情况。
1 实验方法
采用的实验材料为304不锈钢圆柱,其化学成分 (质量分数,%) 如下:C 0.046、Si 0.57、Mn 1.22、P 0.046、S 0.005、Ni 8.01、Cr 18.06、Fe 余量。将其封装在双组份环氧树脂中,一端用铜导线引出,作为工作电极,工作面积为0.317 cm2。工作电极表面用SiC砂纸逐级打磨至2000#,然后镜面抛光至1 μm。最后用去离子水清晰后干燥待用。电解质溶液分别为硫酸溶液 (pH=1.4)、0.2 mol/L醋酸钠缓冲溶液 (pH=5.4) 和0.2 mol/L硼酸缓冲溶液 (pH=9.4或13.4),pH值通过VWR symphony pH计在室温下测得。实验中所有使用的化学药品都为分析纯试剂。实验在室温下进行,溶液温度控制在25±1 ℃。
在电化学测试前,先向反应池内通入高纯氩气 (99.99%) 2 h排除溶液中的氧气,在实验过程中始终通入小流量的氩气保持溶液中氩饱和。参比电极和辅助电极分别为饱和甘汞电极 (SCE) 和铂网。所有的电化学测试都是通过Gamry PCI4工作站进行。在动电位极化实验中,电位扫描速率为0.1667 mV/s。在恒电位极化实验中,恒电位极化6 h后,依次进行电化学阻抗谱 (EIS) 测试和Mott-Schottky (M-S) 测试。EIS扫描频率范围为5×103~10-1 Hz,交流扰动幅值10 mV。M-S所选用的频率为1 kHz,电位以20 mV/s的速度从钝化膜生长电位逆向 (电位更负的方向) 扫描到-1.0 VSCE。实验中配合使用CorrWare/CorrView软件来收集实验数据。获得的阻抗数据通过Igor软件对PDM的模型参数进行优化。
2 结果与讨论
2.1 PDM 模型建立
图1
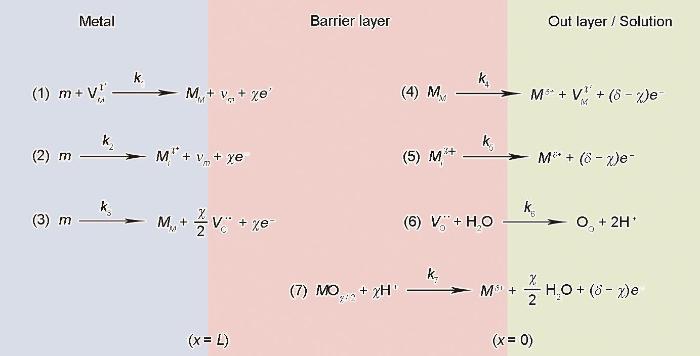
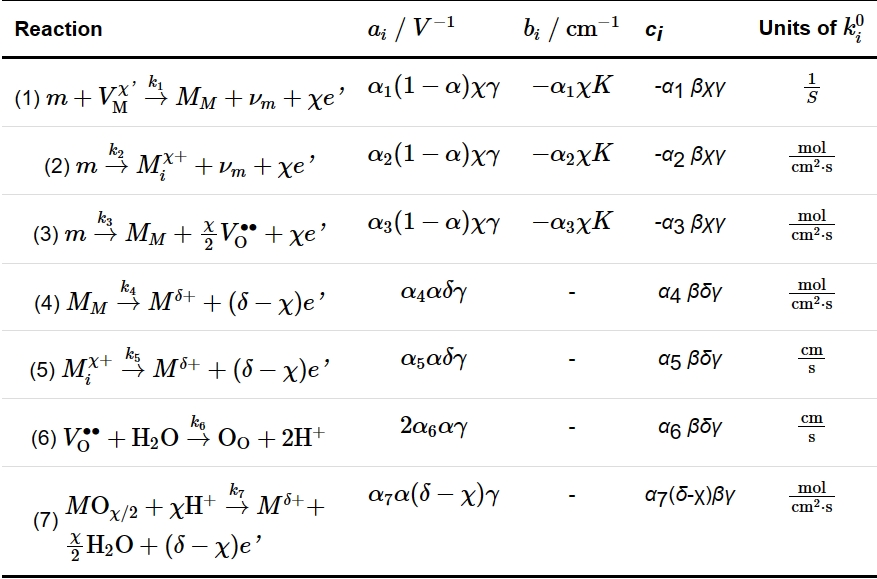
图1 PDM中假设的表示点缺陷产生和湮灭的界面反应
Fig.1 Interfacial defect generation/annihilation reactions happened hypothetically in the growth of anodic barrier oxide films according to PDM. For the symbols, m is metal atom, 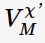 is cation vacancy on the metal sublattice of the barrier layer,
is cation vacancy on the metal sublattice of the barrier layer, 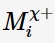 is interstitial cation,
is interstitial cation, 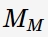 is metal cation on the metal sublattice of barrier layer,
is metal cation on the metal sublattice of barrier layer, 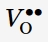 is oxygen vacancy on the oxygen sublattice of barrier layer.
is oxygen vacancy on the oxygen sublattice of barrier layer.
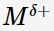
式中,ε是阻挡层内的电场强度,n是钝化膜/溶液界面的溶解反应中H+的动力学级数,α和β分别表示穿过钝化膜/溶液界面的电位降与V和pH的相关系数,V为外加电位。γ=F/RT,F、R和T分别代表Faraday常数、气体常数和温度。根据图1中的反应 (3) 和 (7),钝化膜厚度 (L) 与时间 (t) 之间的关系如
因此,电流密度与电位和钝化膜的厚度的关系可用
在电化学阻抗谱中采用的是正弦变化的交流信号,因此δV=ΔVe jωt,δL=ΔLe jωt,那么Faraday导纳可表示为:
需要注意的是阻挡层内缺陷的电子特征会影响点缺陷在其内的分布。阳离子空位是电子受主,当它为主要缺陷时阻挡层是p型半导体;而阳离子间隙或氧空位是电子施主,当它们是主要缺陷时,阻挡层是n型半导体。从电化学阻抗数据中获得的动力学参数能确认阻挡层内的缺陷浓度及其电子特征。
2.2 电化学测试与PDM分析
图2所示为304不锈钢在不同pH溶液中的动电位极化曲线。在酸性溶液中钝化区间为-0.2~0.8 VSCE (pH=1.4) 和0~1.1 VSCE (pH=5.4),碱性溶液中的钝化区间为-0.6~0.8 VSCE (pH=9.4) 和-0.8~0.5 VSCE (pH=13.4)。随着溶液pH增加,钝化区域向电位负方向移动。在钝化区间选取几个电位,形成表面稳定膜并进行电化学阻抗测试。图3所示为304表面稳态钝化电流与所施加电压的关系。可以看出,施加电压不会对稳态电流数值产生影响,表明阻挡层内的主要缺陷是n型半导体,这通过之后的M-S测试也可以证明。图3中的小插图是6 h恒电位极化时电流密度随时间变化的关系图,在所施加电压下电流密度随时间变化保持恒定表明阻挡层的生长和溶解是同时进行的且达到平衡[14]。
图2
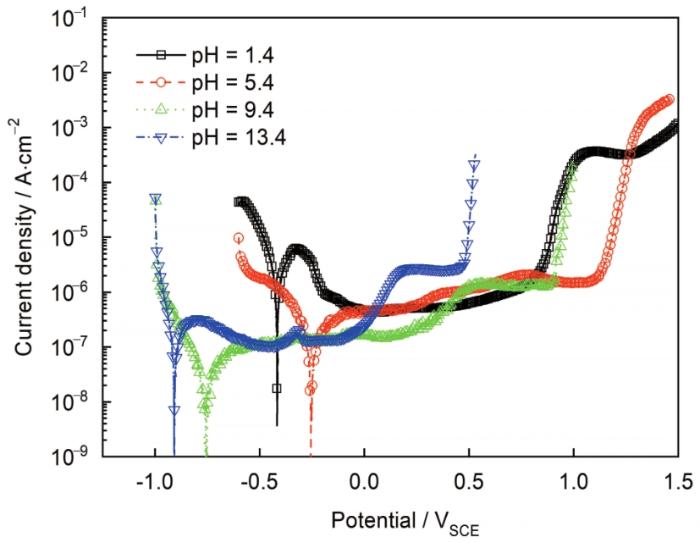
图2 304不锈钢在不同溶液中的动电位极化曲线
Fig.2 Potentiodynamic polarization curves for Type 304 stain steel in the test solutions with different pH values
图3
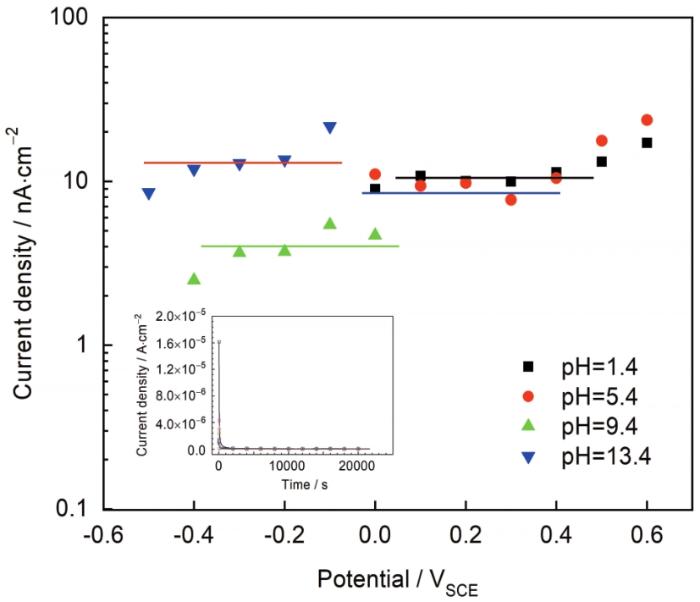
图3 304不锈钢在不同溶液中的稳态 (恒电位极化) 电流密度与电位及电流随时间的曲线
Fig.3 Steady state (potentiostatic) current densities of 304 stainless steel in the test solutions with different pH values as a function of oxide formation potential. The inset shows the current vs. time curves
M-S测试可以用来分析半导体的电子特征,还可以定量的计算出半导体的缺陷密度等。p型和n型半导体中电荷容量可通过以下方程表示:
式中,ZIm是阻抗的虚部,ω=2πf。值得一提的是,M-S分析假定了氧化膜内施主密度的均匀性[17],但是已有的研究[17, 19~21]表明这个假设通常是不成立的,因此本研究中M-S分析是半定量分析。图4a, c, e, g所示为304不锈钢在不同pH溶液中钝化膜空间电荷电容与电位的关系。由图可知,在相应实验条件下,当304不锈钢处于钝化区间时,钝化膜电容平方的倒数与电压呈正比例关系,那么根据M-S理论,304不锈钢表面钝化膜呈n型半导体特征。因此,可以认为在金属/钝化膜界面处的主要缺陷是阳离子间隙或氧空位。图4b, d, f, h所示为在不同电位下形成的钝化膜中的施主密度。本文中计算出的施主密度量级为1021 cm-3,与文献[4]的结果相符,并且施主密度随成膜电位升高而降低的趋势也与文献[16,17]一致。因此,施主密度与成膜电位的关系可由
式中,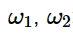 和b是常数,它们的值可由实验获得。图4b, d, f, h示出了实验结果的拟合曲线。由图可以看出施主密度随着溶液pH值的升高而明显降低。根据PDM理论,随着pH的升高,膜/溶液界面的间隙溶解速率降低,载流子密度降低。需要注意的是,在pH=13.4的溶液中没有观察到指数下降关系。
和b是常数,它们的值可由实验获得。图4b, d, f, h示出了实验结果的拟合曲线。由图可以看出施主密度随着溶液pH值的升高而明显降低。根据PDM理论,随着pH的升高,膜/溶液界面的间隙溶解速率降低,载流子密度降低。需要注意的是,在pH=13.4的溶液中没有观察到指数下降关系。
图4
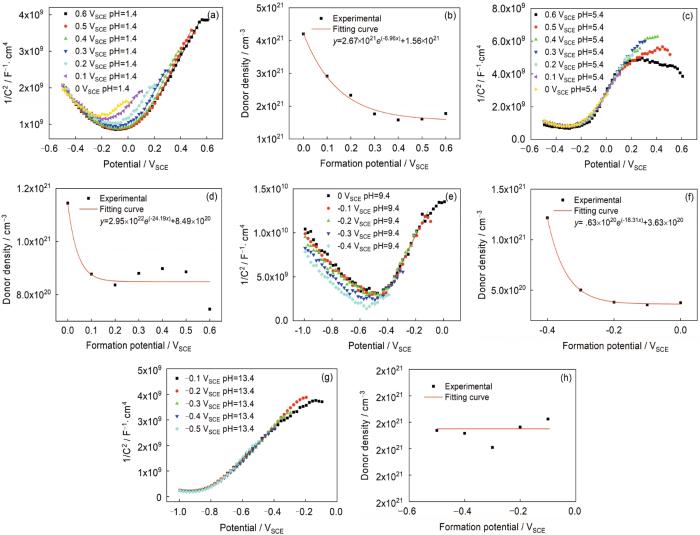
图4 304不锈钢在不同pH溶液中施加不同恒电位极化6 h后的Mott-Schottky曲线和阻挡层的施主密度
Fig.4 Mott-Schottky plots (a, c, e, g) and donor densities (b, d, f, h) for the barrier layer formed on 304 stainless steel passivated for 6 h at different formation potentials in pH 1.4 sulfuric acid solution (a, b), pH 5.4 acetate buffer solution (c, d), pH 9.4 borate buffer solution (e, f) and pH 13.4 H3BO3+NaOH solution (g, h)
在不同溶液条件下对304不锈钢施加恒电位后进行电化学阻抗分析。在本研究中,在使用阻抗谱前,对阻抗数据的可靠性进行了实验和理论的校验。如图5所示,数据点分别表示频率从高到低 (红色圆形) 扫描的和从低到高 (黑色的正方形) 扫描的阻抗数据,可以看出两个方向的扫描结果完全重合没有出现迟滞。实线表示通过K-K转换获得的理论曲线,可见实验和理论计算也具有很好的一致性。通过以上分析可以确定,本实验条件下钝化膜系统符合线性系统要求,并且具有很好的稳定性。在本实验中使用的阻抗数据都进行了以上所述相同标准的校验,从而保证后面分析结果的准确性。
图5
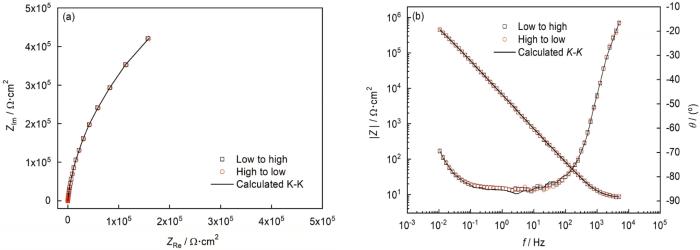
图5 304不锈钢在pH=1.4溶液中0.5 VSCE恒电位极化后的EIS和K-K变换曲线
Fig.5 EIS plots (a) and K-K transforms (b) for 304 stainless steel at a potential of 0.5 VSCE in pH 1.4 solution
通过遗传算法 (GDE),将PDM在实验获得的阻抗数据上进行最优化计算,可以拟合出不锈钢腐蚀反应的动力学参数 (比如,反应速率常数,传输系数等),并且计算值与实验值相符合[13, 25]。在分析电化学阻抗数据时,采用的等效电路图如图6所示。图7b Bode图在低频区是一条直线 (恒相位角阻抗),对电位不敏感。低频阻抗的恒相位角特性是氧化膜中缺陷迁移的结果,主要是在电场作用下的迁移 (即运动通过迁移而非扩散)。阻抗轨迹对施加电位不敏感表明钝化膜内的电场强度与成膜电位无关,这是PDM重要假设之一,即缺陷在阻挡层内传输的驱动力与所施加的电压无关。从物理角度来讲,由于阻挡层内电子和空穴的Esaki隧穿缓冲效应,施加的电位与阻挡层内的场强无关[10, 23]。这也证明了PDM的恒定电场强度的假设。
图6
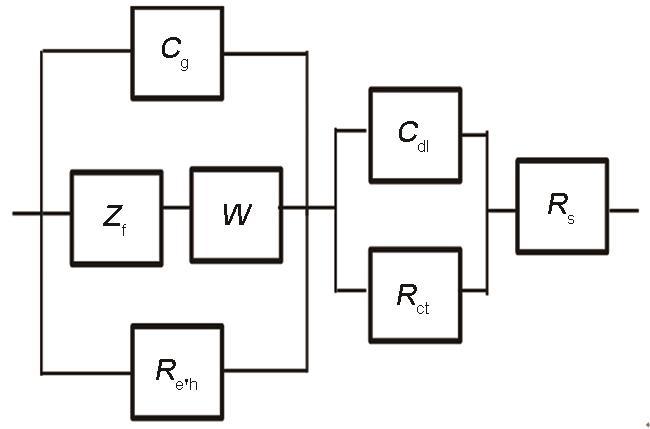
图6 拟合阻抗数据的等效电路图
Fig.6 Equivalent circuit used to fit the experimental data of EIS
图7
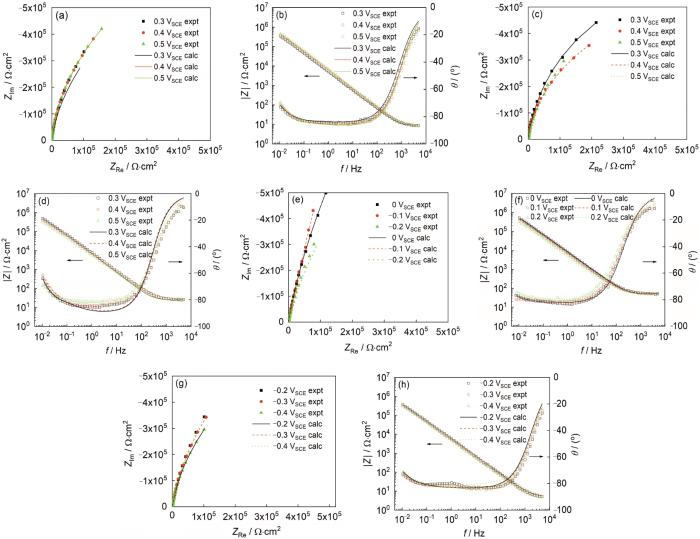
图7 304不锈钢在不同溶液中施加不同电位极化后的EIS图
Fig.7 Nyquist (a, c, e, g) and Bode (b, d, f, h) plots for 304 stainless steel in pH 1.4 sulfuric acid solution (a, b), pH 5.4 acetate buffer solution (c, d), pH 9.4 H3BO3+NaOH solution (e, f) and pH 13.4 H3BO3+NaOH solution (g, h) at different applied potentials
表2 304不锈钢在pH=1.4溶液中不同钝化膜形成电位下PDM最优化模型参数值
Table 2
表3 304不锈钢在pH=5.4溶液中不同钝化膜形成电位下PDM最优化模型参数值
Table 3
表4 304不锈钢在pH=9.4溶液中不同钝化膜形成电位下PDM最优化模型参数值
Table 4
表5 304不锈钢在pH=13.4溶液中不同钝化膜形成电位下PDM最优化模型参数值
Table 5
表2~5中列出了计算的钝化膜内层的厚度。随着极化电位的增大,计算的阻挡层厚度也呈增加趋势。在本研究中,304不锈钢表面的钝化膜内层厚度计算结果为1.24~3.33 nm。这与文献报导值 [26~29]相比数值较小,本文计算膜厚与文献测量膜厚之间的差异可能是由于实验测量的膜厚包括多孔腐蚀产物层 (钝化膜外层) 造成的,而外层通常比致密阻挡层厚,而电化学测试响应信号几乎全部由致密阻挡层贡献[29]。表中所得的钝化膜的厚度对应不同的施加电位,以电位为横坐标钝化膜厚度为纵坐标求斜率可估算出不同pH条件下钝化膜生长速率,然后求取平均值得出生长速率为2.94 nm·V -1,略大于室温下钝化膜生长速率1.9~2.5 nm·V -1 [5]。同样,这里计算出的稳态电流密度 (Iss ) 基本上与电位无关,并且接近于图3中的实验值。基于PDM理论,在金属/钝化膜界面生成的点缺陷向钝化膜/溶液界面传输的驱动力主要是电场。此外,计算所得间隙阳离子的扩散系数值约为10-18~10-20 cm2·s-1,符合文献的报导值[26~29]。
3 结论
动电位极化实验表明304不锈钢在pH 1.4~13.4溶液中均有较宽的钝化区间。在稳态条件下,电流密度不受施加电位的影响,而钝化膜厚度以2.94 nm·V -1的速度随着电位的增加而增厚。Mott-Schottky测试表明了304不锈钢表面钝化膜是n型半导体,并计算出了施主密度在不同pH和电位条件下的数值,计算结果表明阻挡层内的施主密度随着成膜电位增加呈指数型下降,其值也随着pH值的增加而降低。
通过点缺陷模型优化了实验获得的304不锈钢钝化膜电化学阻抗谱数据,推导出其在溶液中钝化状态的反应动力学参数的数值解,利用这些参数可以预测稳态和瞬态的钝化膜生长过程。本研究获得的动力学数据表明,点缺陷模型能够合理解释304不锈钢的钝化状态,该模型可以预测不锈钢在特定条件下长期的均匀腐蚀行为。
致谢
感谢加州大学伯克利分校Digby Macdonald教授对论文内容的讨论与指导。
免责声明:本网站所转载的文字、图片与视频资料版权归原创作者所有,如果涉及侵权,请第一时间联系本网删除。

官方微信
《腐蚀与防护网电子期刊》征订启事
- 投稿联系:编辑部
- 电话:010-62316606
- 邮箱:fsfhzy666@163.com
- 腐蚀与防护网官方QQ群:140808414