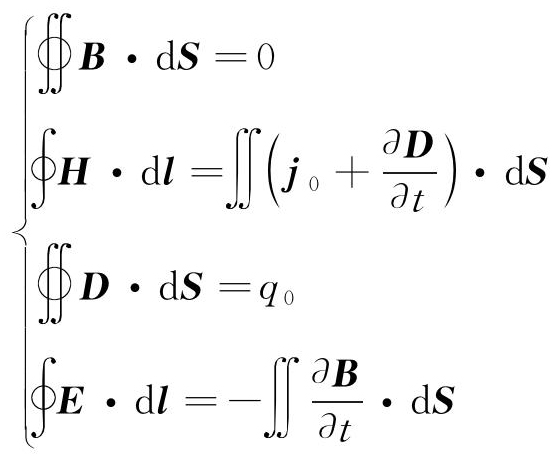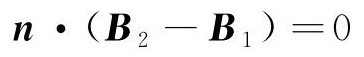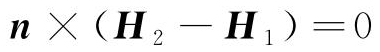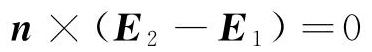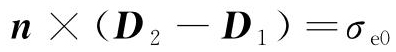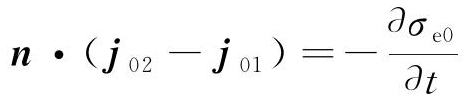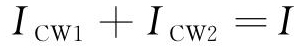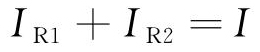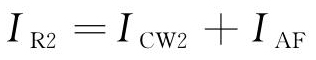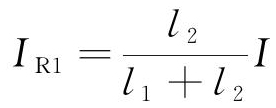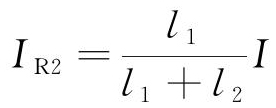随着经济的发展和能源需求的增加,电气化铁路和埋地油气管道建设大幅增加,受空间及环境因素的制约,二者不可避免会形成交叉或平行的情况。当电气化铁路与埋地管道相互并行交叉时,可能通过电磁耦合、电阻耦合、电容耦合等方式对埋地管道产生交流干扰,可能使管道产生交流腐蚀甚至击穿管道防腐蚀层[1-2]。目前,国内外已经出现大量管道受交流电气化铁路产生电磁干扰的实例[3-6]。美国某条有阴极保护的管道与电气化铁路长距离并行（二者最小距离为150 m）,管道的干扰电压可达33 V,最低也有5 V[7]；德国某条管道[8]与某15 kV电气化铁路交叉并行,近年检测发现管道发生两处交流干扰引起的腐蚀,且这两处的管道断电电位负于-1.0 V（相对于铜/硫酸铜参比电极,CSE）；国内,某天然气管道[9]与城市地铁存在公共走廊,交流干扰电压达44.1 V；嘉兴段管道[10]与高铁近距离并行并交叉,管道多处交流干扰超标。由于电气化铁路而产生的交流干扰问题给管道带来了巨大的经济损失,已成为研究热点[11-17]。 

在分析电气化铁路对埋地管道交流干扰时,往往采用等效电路的方法推导计算公式[18]进行计算并解决问题。等效电路法将电气化铁路等效为各种电力元件,根据电磁场理论,分别考虑电阻耦合和电感耦合,推导管道交流干扰电压的计算公式。然而,该方法不能综合考虑电阻耦合和电感耦合的影响,不适用于系统部件多、环境复杂多变的情况,且计算精度较低。近年来数值仿真技术发展迅速,在电磁仿真等领域得到了广泛的应用,同时广泛用于分析电气化铁路产生的交流干扰[19-22]。许多学者对数值模拟技术进行了深入的研究。唐伟等[23]开发了一款交流干扰计算软件,用于研究并有效防止电气化铁路对管道所产生的具体影响；OSBORNE等[24]运用数值模拟软件对欧洲某条受交流干扰的管道进行干扰预测和缓解设计。由于高速列车处于持续运动状态,其位置变化将对管道的交流干扰产生影响,最终影响交流干扰缓解措施的实施。因此,有必要研究和阐明高速列车的位置对管道干扰的影响,以期为后期干扰的准确防护提供参考。 

笔者综合运用数值模拟技术结合理论分析,研究了电气化铁路与管道不同交叉点时单一列车在不同位置,管道的交流干扰分布情况以及各导体上电流分布。以明确管道干扰峰值出现的位置以及产生机理。同时,开展了现场测试工作,验证了模型的有效性,以期为高铁交流干扰防护提供参考和借鉴。 

1.   计算原理及模型

1.1   计算原理

空间中的电磁场相互作用规律满足Maxwell方程组,在均匀、线性、各向同性的非磁性媒质中,其积分形式如式（1）所示。 

式中：B为磁感应强度矢量；dS为面微元；H为磁场强度矢量；dl为线微元；j0为传导电流密度矢量；D为电位移矢量；E为电场强度矢量；q0为自由电荷量；t为时间。 

只有在边界条件已知的情况下求解Maxwell方程才能得到唯一解。在两种不同的介质分界面上,由于介电常数、磁导率和电导率不同,对应三组边界条件[25]。 

1.1.1   磁介质界面上的边界条件

在如图1所示的扁状高斯面,应用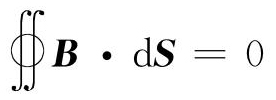得到磁感应强度法向分量连续性的边界条件如式（2）所示。 

图  1  介质界面上的边界条件：法向分量

Figure  1.  Boundary conditions at the interface of media: normal component

图2所示为狭长矩形闭合环路,认为介质界面上没有传导电流,,得到磁场强度切向分量连续性条件如式（3）所示。 

图  2  介质界面上的边界条件：切线分量

Figure  2.  Boundary conditions at the interface of media: tangential component

1.1.2   电介质界面上的边界条件

在高斯面上,认为介质界面上没有自由电荷（即q0=0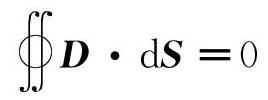）,,得到电位移法向分量连续性边界条件如式（4）所示。 

在闭合环路上,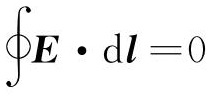,得到电场强度切向分量连续性边界条件如式（5）所示。 

1.1.3   导体界面上的边界条件

对于导体表面,可能存在自由电荷积累,利用高斯定理得到电位移矢量法线分量的边界条件如式（6）所示,其中σe0是导体分界面上的自由电荷面密度。 

此外,在高斯面上运用电流的连续方程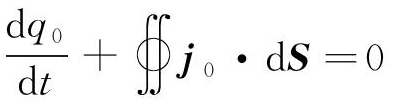,得到传导电流密度法向分量的边界条件如式（7）所示。此外,在导体表面边界条件下,式（2）和式（5）也成立。 

目前,对于一定边界条件下的Maxwell方程求解,主要有以矩量法（MoM)[25-26]为代表的积分类方法和以时域有限差分法（FDTD)[27]为代表的微分类方法。笔者采用加拿大SES公司开发的CDEGS软件进行计算机仿真,该软件基于矩量法进行计算求解,是通过离散和检验两个过程将一个连续方程转化为离散的代数方程组,然后再对离散的矩阵方程求解得到目标的电场或磁场分布[28-31]。 

1.2   计算模型及参数

本次计算数据来源为北京地区某高速铁路对临近燃气管道的交流干扰。为了探寻高速铁路对埋地管道的干扰规律,笔者去除其他因素的影响（例如高速铁路与管道的相对位置和间距）,对实际模型进行简化。高速铁路采用自耦变压器（AT）供电模式,牵引变电站（TPSS）位于最左侧,牵引变电站配有一个AT。距离牵引变电站10 km和20 km处,分别有一个AT所。TPSS, AT1和AT2处均有一个4 Ω的站场接地网与铁轨（相Rail）连。如图3所示,管道长40 km,高速铁路长20 km,并行段长20 km。管道与高速铁路并行,在TPSS和AT1中点或AT1和AT2中点管道与高速铁路垂直交叉,间距为15 m。 

图  3  计算模型相对位置关系示意图

Figure  3.  Schematic diagram of the relative position relationship of the calculation model

由图4可见,牵引网（简称CW）在铁路中心线正上方距离地面6.3 m,正馈线（简称AF）在左侧4.4 m,高8.5 m。铁轨分布在中心线两侧,距离地面1 m。 

图  4  计算模型界面示意

Figure  4.  Schematic diagram of the interface of the calculation model

1.2.1   高铁参数

高铁牵引变电站站采用2个25 kV电压源模拟,频率为50 Hz。在牵引变电站以及2个AT所位置（共3处）分别绘制自耦变压器,变压比为2∶1。在牵引变电站以及2个AT所位置绘制接地网（尺寸为10 m×10 m）,接地网与铁轨直接相连。高铁各导体电学参数如下：接触网纵向电阻0.183 Ω/km,回流线纵向电阻0.096 Ω/km,铁轨纵向电阻0.45 Ω/km,铁轨泄漏电阻15 Ω·km。列车采用等效阻抗替代,等效电阻为62.5 Ω·km（列车的工作电流约为400 A）。 

1.2.2   管道参数及土壤电阻率

管线钢采用X70钢,外部包覆3PE防腐蚀层,电阻率1.344×10-7 Ω·m,相对磁导率300,外径1 016 mm,壁厚10mm,防腐蚀层面电阻率100 000 Ω·m2,管道埋深1.5 m。按照ISO 18086-2019 Corrosion of metals and alloys - Determination of AC corrosion - Protection criteria标准要求,交流腐蚀风险的评价采用1 cm2缺陷上的交流电流密度进行。因此,在管道表面每50 m绘制1个1 cm2的破损点,用于计算该处位置的交流电流密度。 

采用均一土壤模型,土壤电阻率为55 Ω·m。 

1.3   计算内容

本工作主要计算以下工况下管道的交流电压分布情况以及各导体电流分布：（1）管道与高速铁路系统在牵引变电站和AT所中段交叉时,列车行驶位置（0~20 km）对管道干扰的影响；（2）管道与高速铁路系统在两个AT所中段交叉时,列车行驶位置（0~20 km）对管道干扰的影响；（3）铁轨泄漏电阻变化（1~200 Ω·km）对管道干扰的影响。列车计算算例见表1。 

高铁对埋地管道的干扰主要来自于其产生的电磁场。改电磁场主要有两个方法：（1）各个导体（AF, CW, Rail）与管道之间的间距不同,称之为位置不平衡；（2）AF, CW以及Rail之间电流的向量和不为0,称之为电流不平衡。 

2.   结果及讨论

2.1   管道与高铁在5 km处交叉时列车运行位置对管道干扰的影响

由图5可见,列车运行时,管道上的干扰电压曲线不断变化。不论列车处于什么位置,管道干扰在5 km附近（即交叉点附近）始终存在一个峰值。当列车刚离开TPSS,管道所受干扰很低。当列车运行到TPSS与AT1中间以及AT1与AT2中间时,干扰较高。当列车运行到TPSS与AT1之间时,管道干扰出现三个峰值,即10 km（高铁与管道并行起点）,交叉点附近和30 km（高铁与管道并行终点）；当列车运行到AT1与AT2之间时,管道干扰出现四个峰值,即10 km(高铁与管道并行起点）,交叉点附近,列车所在位置附近和30 km(高铁与管道并行终点）。当列车在AT1和AT2附近时,管道干扰只有2个峰值,为列车位置及交叉点附近。 

图  5  列车运行至不同位置时管道沿线交流电压分布

Figure  5.  AC voltage distribution along the pipeline when the train runs to different positions: (a) 0.01 km; (b) 5 km; (c) 9.99 km; (d) 10.01 km; (e) 15 km; (f) 20 km

为了分析列车不同位置时,干扰曲线不同的原因。计算了CW、AF以及Rail铁中的电流分布情况。当列车在TPSS与AT1之间运行时,理想情况下各个导体中的电流分布如图6所示。根据基尔霍夫定律,忽略泄漏阻抗,且认为导体纵向阻抗与长度成正比,得到式（8)~(12）。由式（10）和（12）可知,当列车靠近TPSS时,L1近似等于0,因此IR2、IAF和ICW2都近似等于0,见图6（a）。管道高铁并行段基本无电流,感应耦合小,管道的交流干扰小。 

图  6  列车运行至不同位置时导体的电流分布

Figure  6.  Current distributions in conductors when the train runs to different positions: (a) 0.01 km; (b) 5 km; (c) 9.99 km; (d) 10.01 km; (e) 15 km; (f) 20 km

当列车运行到5 km时,根据式（8)~(12）可知,理论上ICW1与IR1、IAF之和相等,IR2与ICW2, IAF之和相等。其对外产生的综合电磁场大小取决于CW、AF以及Rail位置不平衡以及Rail泄漏部分电流产生的电流不平衡。由图7可见,列车前后铁轨上的电流方向相反,因此列车前后不平衡电流方向也相反,这导致对外磁场方向相反,产生的纵向电动势也相反,在此处会出现干扰峰值。 

图  7  列车在TPSS与AT1区间时的电流分布示意

Figure  7.  Schematic diagram of current distribution when the train is in the section between TPSS and AT1

由图6可见,由于铁轨会向大地中泄放电流,因此铁轨中的电流变化较大。如：在TPSS附近ICW1比IR1、IAF之和高28 A,因此在实际工程中,CW、AF以及Rail的电流差距会产生额外的磁场强度,对管道所受干扰产生影响。由此可见,此时交流干扰由CW、AF以及Rail之间的位置不平衡和电流不平衡共同作用。 

当列车运行到靠近AT1的上游时（9.99 km）,电流分布示意见图7。当列车运行到靠近AT1的下游时（10.01 km）,电流分布示意见图8。列车在AT1上游靠近AT1时,IR1基本为0,CW和AF电流大小相等方向相反,为列车电流的1/2。列车在AT1下游靠近AT1时,IR2基本为0,TPSS至AT1区间的电流与列车在9.99 km时相同。因此,两种情况下管道所受干扰变化不大,即列车在AT所前后管道所受干扰不发生明显变化。由于此时铁轨中电流流动距离很短（10 m）,基本无泄漏,因此电流不平衡的影响很小。交流干扰主要由CW和AF的位置不平衡引起,干扰峰值出现在高铁有电流段（TPSS至AT1）的起始点和终点。对比图6（c）与图6（b）,可见纯位置不平衡引起的干扰为6.6 V。而位置不平衡和电流不平衡叠加作用下的干扰可达39.2 V。这表明,该工况下电流不平衡引起的交流干扰远大于位置不平衡引起的干扰。 

图  8  列车在AT1与AT2区间时的电流分布示意

Figure  8.  Schematic diagram of current distribution when the train is in the section between AT1 and AT2

当列车运行到15 km出现干扰峰值,此时TPSS至AT1段有较大的电流,但由于CW与AF线距离较近,铁轨中电流很小,因此TPSS至AT1段引起的干扰增加效应不明显；而列车运行5 km时,AT1至AT2段基本无电流,但由于此时机车位于交叉点,CW、AF以及Rail之间的位置不平衡和电流不平衡共同作用导致干扰增加更加明显,因此列车运行到5 km时干扰更大。 

当列车运行到20 km时,列车与AT2的距离为0,铁轨中无电流。交流干扰由TPSS至AT1以及AT1至AT2段,CW与AF的位置不平衡引起。由于并行距离长,因此干扰程度大于列车在9.99 km的时候。 

此外,不论列车处于什么位置,管道干扰在5 km附近（即交叉点附近）始终存在一个峰值。以图7为例,当列车行驶在AT1附近时,理论上ICW1与IR1、IAF之和相等（示意见图9）,根据图4可见,由于在交叉点前AF距离管道更近,三者因位置不平衡在管道形成的感应电动势ECW1大于ER1与EAF之和；而在交叉点后CW距离管道更近,三者因位置不平衡在管道形成的感应电动势ECW1小于ER1与EAF之和,因此在交叉点处始终存在一个峰值。 

图  9  CW, AF和Rail的电流示意

Figure  9.  Current vector diagram for CW, AF and Rail

综上所述,列车在铁路上运行并获取电流时,管道上对应列车所在位置附近会产生交流干扰峰值,管道与高铁交叉点也会产生交流干扰峰值。当列车运行在AT1至AT2之间时,铁轨上存在电流,由于铁轨与CW和AF位置相差较远,同时铁轨上会有一部分电流泄漏进入大地。因此,在位置不平衡和电流不平衡的双重作用下,管道受干扰比较明显。而当列车处于TPSS或AT所时,即使列车获取电流,由于大部分电流都经由AF进行回流,铁轨中电流很小,管道所受干扰较低。 

2.2   管道与高铁在15 km处交叉时列车运行位置对管道干扰的影响

计算列车在不同位置时,管道沿线交流干扰电压分布如图10所示。由图可见,管道干扰情况与交叉点在5 km处的基本一致,不同之处在于：当列车运行在TPSS和AT1之间时,交叉点附近并未出现干扰峰值,这是因为此时AT1到AT2之间并未供电。当列车运行在AT1附近时,管道干扰峰值出现在列车位置和10 km处。当列车运行在AT2附近时,管道干扰位置出现在机车位置、交叉点和10 km处。 

图  10  列车运行至不同位置时管道沿线交流电压分布

Figure  10.  AC voltage distribution along the pipeline when the train runs to different positions: (a) 0.01 km; (b) 5 km; (c) 9.99 km; (d) 10.01 km; (e) 15 km; (f) 20 km

CW、AF以及Rail中的电流分布情况,见图11。列车运行在15 km时,管道干扰电压达到最大值40.81 V,高于机车运行在5 km且交叉点为5 km时的39.21 V,但增幅不大。这是因为此时TPSS至AT1段有比较大的电流,而列车在5 km时AT1至AT2段基本无电流。但是,由于CW与AF线距离较近,铁轨中电流很小,因此TPSS至AT1段引起的干扰增加效应不明显,相较于列车在5 km时,管道干扰水平有所增加,但是增幅不大。列车运行到该位置处,交流干扰主要由于TPSS至AT1段的CW和AF的位置不平衡,以及AT1至AT2段CW、AF以及Rail之间的位置不平衡和电流不平衡共同作用。 

图  11  列车运行至不同位置时导体的电流分布

Figure  11.  Current distributions in conductors when the train runs to different positions: (a) 0.01 km; (b) 5 km; (c) 9.99 km; (d) 10.01 km; (e) 15 km; (f) 20 km

2.3   铁轨泄漏电阻对管道干扰的影响

铁轨泄漏电阻是影响交流干扰的重要因素,初始设置铁轨泄漏电阻为15 Ω·km,改变铁轨泄漏电阻为1~200 Ω·km,计算模型采用交叉点在15 km且列车也运行在15 km处（此时管道干扰最大）,计算铁轨泄漏电阻对管道干扰的影响,由图12可知,随着铁轨泄漏电阻的增大,管道受到的交流干扰减小。由图13可见,管道的最大干扰电压随铁轨泄漏电阻的增大先急剧降低,然后趋于平稳,因此在铁轨泄漏电阻不大时,小范围改变铁轨泄漏电阻会对管道干扰产生很大影响。 

图  12  不同铁轨泄漏电阻下的管道沿线干扰

Figure  12.  Interference along the pipeline with different rail leakage resistances

图  13  最大干扰与铁轨泄漏电阻的关系

Figure  13.  Relation between maximum interference and leakage resistance of rail

由图14可知,随着铁路泄漏电阻增大,CW和AF中的电流基本不变,铁轨泄漏进入土壤的电流变少而导致电流不平衡的影响变小,同时由于铁轨泄漏电流的减少,CW、AF以及RAIL位置不平衡的影响也变小。 

图  14  不同铁轨泄漏电阻下的导体电流分布

Figure  14.  Current distribution of conductors with different rail leakage resistance: (a) 1 Ω·km; (b)10 Ω·km; (c) 15 Ω·km; (d) 50 Ω·km; (e) 100 Ω·km; (f) 200Ω·km

3.   实际现场测试验证

为了验证计算模型的准确性,对研究得到的规律性结论进行论证,针对北京地区某实际燃气管道受高铁干扰的情况进行了现场测试。并将测试结果与计算结果进行比对,验证计算的准确性。 

某燃气管道和高铁的位置关系如图15所示,燃气管道北侧为起点,南侧为终点。管道沿线距离起点0,1.4,2.4,3.4,4.7,6.1,6.7,8.0 km处的交流干扰电压进行同步监测。 

图  15  现场测试管道与高铁的相对位置关系及现场测试情况

Figure  15.  Relative location relationship between the pipeline and the high-speed railway during field testing and the situation of field testing

记录了列车运行到3.4,4.7,6.7 km时,管道沿线的交流电压分布,见图16。由图16可见,管道沿线交流电压最大值位置随着机车运行而发生改变,且基本与列车所处位置重合,这与理论分析结论一致。此外,现场测试结果显示该段管道出现两个峰值点,分别在起始点和列车运行位置,这是因为管道在起始点处与高速铁路开始并行,而在列车运行位置存在电流不平衡及位置不平衡,因此出现峰值。与图5（e）中出现3个峰值不同是因为现场实测管道在南端,连接的长管道起到了接地作用,降低了南端并行段截止处的交流电压。 

图  16  现场测试列车运行到不同位置时管道沿线交流电压分布

Figure  16.  AC voltage distribution along the pipeline when the train runs to different positions during field testing

采用CDEGS计算列车运行到4.7 km时管道的交流干扰水平,并将结果与现场测试结果进行对比。由图17可见,总体上计算所得管道干扰趋势和实测结果相吻合。因此,该计算结果验证了计算模型的合理性。此外,需要注意数值上管道南侧干扰计算结果与实测吻合性较好,北侧吻合性稍差,这可能是北侧更加靠近居民区,管道防腐蚀层破损较多导致该段管道对地电阻降低。 

图  17  现场测试结果与模拟计算结果对比

Figure  17.  Comparison of field testing results with simulated calculation results

4.   结论

（1）列车运行时,管道上对应列车所在位置处会产生交流干扰峰值。这是由于列车前后铁轨上电流方向相反,泄漏电流后AF, CW以及Rail三者之间的不平衡电流方向相反,产生的纵向感应电动势方向相反。因此,在列车运行位置处形成干扰峰值。 

（2）由于交叉点的存在,当交叉点所在分段有供电时,管道在交叉点总会出现一个干扰峰值。 

（3）列车运行至TPSS与AT1中点以及AT1与AT2中点时,管道所受干扰最大。运行至TPSS, AT1以及AT2时,干扰出现谷值。这主要是由于当列车运行至中点时,铁轨上电流比较大,在位置不平衡和电流不平衡的双重作用下,对管道干扰较大。而当列车处于TPSS, AT1以及AT2时,由于大部分电流都经由AF回流,铁轨中电流很小。交流干扰主要由AF和CW之间的位置不平衡引起,因此干扰较低。 

（4）管道上的交流干扰随铁轨泄漏电阻增大而减小,这是因为随着铁轨泄漏电阻增大,铁轨泄漏到大地的电流减少。 

（5）靠近TPSS, AT1和AT2附近的管道除了受到感应耦合外,还受到集中接地网泄漏电流的阻性耦合。但是,阻性耦合与感应耦合的位置不同,导致有些地方干扰增加有些地方干扰降低。