0 前言

再制造通过对退役零件进行专业化修复或升级改造使其质量特性不低于新品零件,是产品残余价值有效重用的重要途径之一[1]。退役零件的失效模式多种多样[2],包括磨损、老化、断裂、裂纹等。不同的失效模式及其失效程度是影响零件能否再制造重用的关键因素之一,快速精确量化表征其失效特征对于退役零件的再制造评价和再制造工艺选择具有重要意义。

零件内部的失效特征多采用超声波无损探伤、电磁波无损探伤、射线检测等[3-5] 技术测量并表征其失效程度。零件表面的失效特征常采用模糊评价法、3D扫描重建法等[6-7]进行表征。其中,模糊评价法通过专家评价结果进行失效特征量化,主观性较大,评价结果不精确。扫描重建法使用3D扫描仪获取零件的三维点云,通过对比分析新旧零件得到其失效特征表征结果,精度高,但需要特定的设备, 成本高,过程复杂,效率低。

图像三维重建一直是计算机视觉中的经典问题,图像三维重建分为多摄像头重建和单摄像头重建[8-9],单摄像头重建方法成本更低,包括由聚焦获取深度(Depth from focus,DFF) [10]、由阴影恢复形状( Shape from shading, SFS) [11]、由运动恢复形状(Shape from motion,SFM) [12]等典型方法,其中,SFM算法具有重建精度高、效率高等特点,是近年来研究和应用的热点算法。 SFM算法应用SIFT、 SURF、 AKAZE等特征检测算法[13-15] 提取序列图像中的特征点,以相同特征点建立假定光度匹配, 并使用RANSCA算法[16]对匹配结果进行优化,且根据后续流程不同,SFM算法可分为增量式SFM和全局式SFM算法。增量SFM算法选取最大相匹配特征点和最佳基线角度的图像对作为初始图像对进行两视图重建,利用三角定位恢复特征点三维坐标,应用光束平差法对坐标进行优化,并逐张加入图像实现多视图重建,得到稀疏点云。陈辉等[17]使用增量SFM算法实现了沙堆的三维重建,并进行了尺寸测量。董建伟等[18] 使用无人机拍照并利用增量SFM算法实现了港口煤堆的三维重建。但是,由于增量式SFM算法在重建过程中逐张加入图像,计算图像中特征点的三维坐标,随着图像数量增加,导致计算误差积累, 相机轨迹闭包处理困难,重建点云产生飘移。

全局式SFM算法的优势在于小基线下可以非常精确估计相对应的两视图旋转,将误差平均分布, 同时减少了光束平差次数,提高了重建效率,但对图像质量和相机内部参数要求更为严格。鲁晨曦[19] 使用全局SFM算法实现了建筑物的三维重建。 MOULON等[20] 对全局SFM算法进行改进,提出了有效的对偶三焦张量估计方法以得到稳定的平移方向,并定义了一种平移匹配方法以恢复相机的几何位置,提高了算法的重建精度。

退役零部件的表面失效模式包括变形、磨损、腐蚀等,其失效量级多为毫米级,失效部分形状不规则,需要完整获取退役零件的全部失效特征,并保证重建点云的闭合性和完整性,且为减少点云处理步骤,增加点云光滑度,需要尽可能减少噪点数量。增量SFM算法存在重建点云中三维点漂移,重建过程中相机闭包处理困难等问题,全局SFM算法误差分布均匀,噪点少,但相机内部参数的精确度有待提升,因此,上述方法都无法直接用于退役零件表面失效特征的三维重建。为此,文中提出了自标定全局SFM算法,使用退役零件图像集构建图像特征点匹配关系,应用光束平差法自标定相机,优化相机焦距、径向畸变参数,结合全局SFM算法完成重建,提高了算法的鲁棒性。为提高零件表面失效特征表征效率,文中提出了基于图像三维重建的退役零件表面失效特征表征方法,由退役零件序列图像快速获得其失效特征信息。

1 自标定全局SFM算法

1.1 相机自标定

被测物体的图像坐标与世界三维坐标转换的准确度很大程度上影响图像三维重建结果的好坏,坐标转换公式如式(1)所示

         (1)

式中,(X W,Y W,Z W )表示三维物体世界坐标,Z C 表示相机坐标,(U,V)表示像素平面坐标,K 为相机内参矩阵,M 为相机外参矩阵,f x、f y 为归一化焦距,s 为倾斜因子,c x、c y 为点在图像坐标系上的坐标,R 表示旋转矩阵,T 表示平移矩阵。式(1) 是针孔相机模型的坐标转换公式,实际情况中还需要考虑相机的径向畸变参数。

由式(1)可知,影响重建精度的主要因素为相机的内参矩阵和外参矩阵,内参矩阵的主要影响因子为相机的焦距和畸变参数,已有研究一般应用张友正提出的相机标定法[21]标定,需要构建相机标靶的图像集,耗时长,适用场景有限,且拍摄图片过程中,相机畸变受温度、风速、气压等外界环境影响,单独的实验室标定数据难以符合实际情况。文中使用退役零件图像集中的退役零件作为标定物,无需单独制作相机标靶进行相机标定。构建图像集时应用同一相机从不同角度获取待重建物体的序列图像, 获取图像间大量匹配点对,应用光束平差算法求解相机焦距和径向畸变参数。相机自标定模型如图1所示。

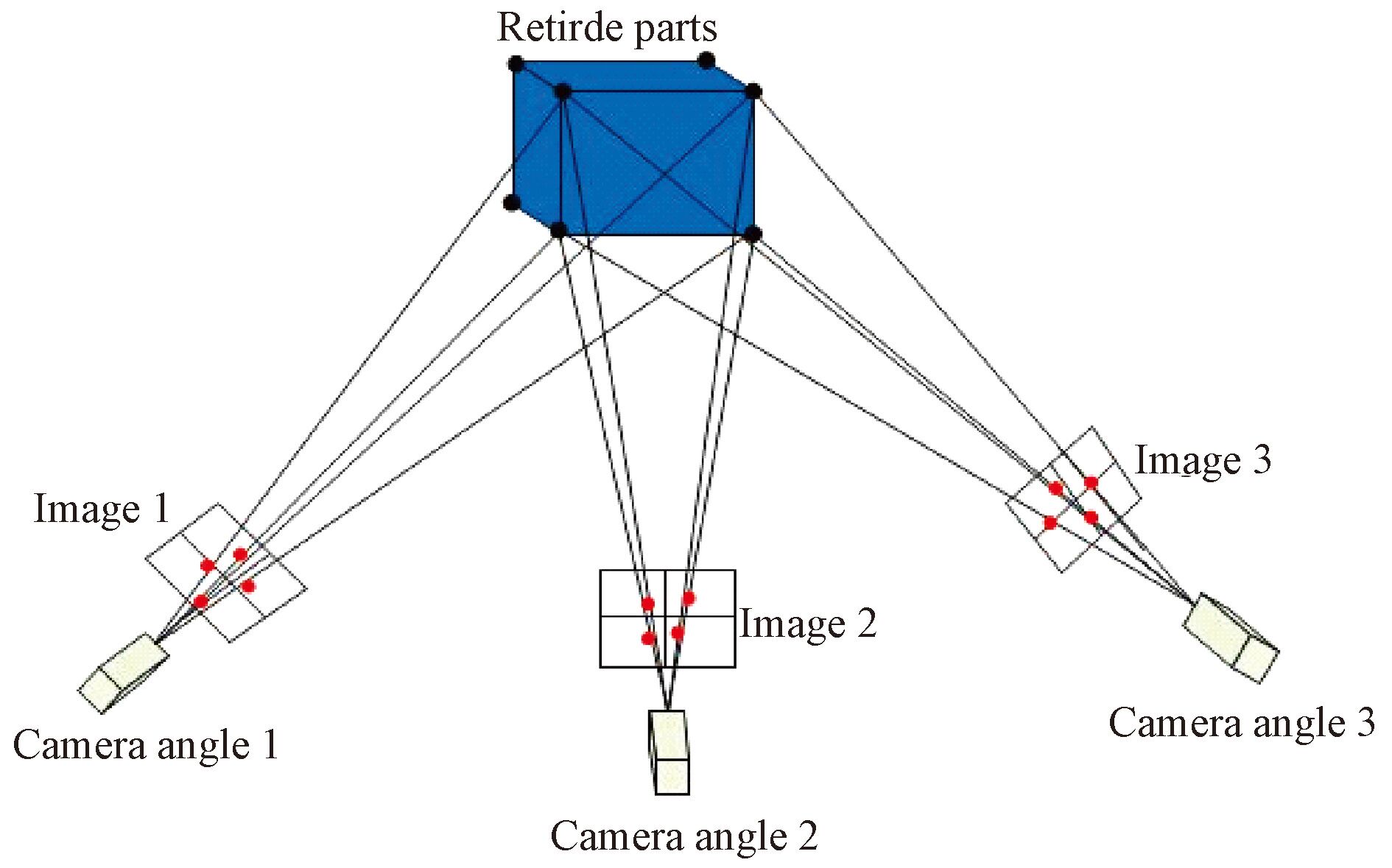
图1 相机自标定模型

根据图片内部的可交换图像文件格式(EXIF) 信息估计相机的焦距,其公式如下。

        (2)

式中,f p 为相机焦距( 像素), f m 为相机焦距( 毫米),w p、 h p 分别表示图像宽度和长度( 像素), ccdw m 为相机传感器宽度(毫米)。应用SIFT算法提取图像中的特征点并建立匹配关系,应用ACRANSAC算法[22]消除误匹配,应用增量SFM算法寻找筛选初始图像对,完成二视图重建和三视图重建,由于参与重建的图像数量少,避免了增量SFM算法累积误差的产生,同时可获取足量特征点的三维坐标,然后应用光束平差算法求解相机的焦距 f p 和畸变,其中,考虑相机模型为针孔径向,相机畸变参数只考虑径向畸变,阶数为三阶, 径向畸变模型如式(3)所示

      (3)

式中,r 为像平面坐标系中点(x,y)与图像中心(x 0, y 0)的像素距离,( x c,y c)为修正后的坐标,k 1、k 2、k 3 为径向畸变系数。对于一个特征点,可在多幅图像上可列出其误差方程

    (4)

式中,

为特征点像素坐标系的修正矩阵,A、B、C 为相机内外参数和特征点三维坐标的偏导数矩阵,X 1、X 2、X 3 为相机内外参数和特征点三维坐标的修正数,

为观测值向量。

根据最小二乘原理可列出式(4)的法方程式

   (5)

式中,P 为特征点观测值的权矩阵。对法方程式消元即可得到关于相机内外参数的非齐次线性方程组,求解得出相机的焦距和三阶径向畸变参数。

1.2 自标定全局SFM算法流程

文中将相机自标定融入到全局SFM算法中,提出了自标定全局SFM算法,其步骤如下。

步骤1:对图像集中的图像进行预处理,获取相机的内参信息,应用SIFT算法提取和匹配图像中特征点,构建图像匹配关系。

步骤2:应用增量SFM算法完成三视图重建,获取三视图间大量匹配点对。

步骤3:应用光束平差算法求解相机焦距和三阶径向畸变参数。

步骤4:以求解的相机内部参数和已经构建好的图像匹配关系为基础,计算每个视图的全局旋转矩阵。

步骤5:计算每个视图的平移矩阵,进行三角定位和整体光束平差得到重建物体的稀疏点云。

步骤6:应用CMVS/PMVS算法得到重建物体的稠密点云。

图2 为文中算法的流程图。

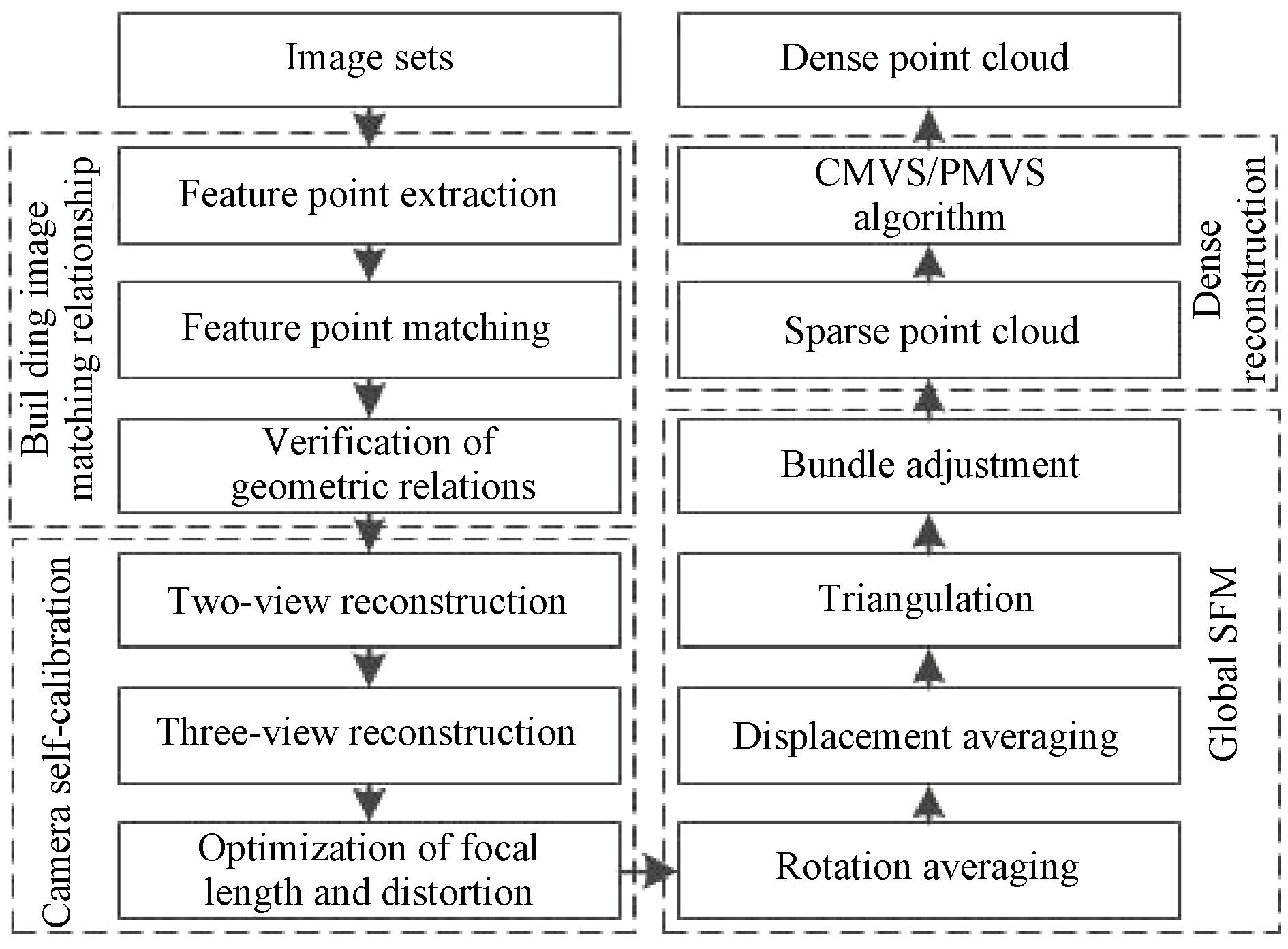
图2 自标定全局SFM算法流程图

2 基于试验的图像重建精度评价

2.1 重建精度评价模型

退役零件三维模型的重建精度受多种因素影响,主要因素包括以下几点。

(1) 重建有效三维点数量占比。退役零件重建三维曲面由退役零件稠密点云中的有效三维点相互连接构成,为了能够使三维点拟合而成的曲面更加致密,需要三维重建算法能够求解出尽可能多的三维点以生成高精度的稠密点云。由于图像中的噪声点和图像对间错误匹配对的存在,重建后的稠密点云中会不可避免的产生噪点,增加逆向工程重建的时间复杂度,如删除不尽,则可能与有效三维点相连接而形成错误的三维曲面,从而引入误差,影响三维模型的表面形状,为了减少上述问题,应使重建有效三维点数量尽可能多,同时,重建有效三维点数量占重建三维点总数的比例应尽可能高。

(2) 点云完整度。由于失效特征在退役零件表面呈随机分布,重建出的退役零件三维模型应尽可能的包含全部的失效特征,这要求在尽可能恢复更多有效三维点的基础上使三维点均匀分布,构成退役零件的完整模型。

(3) 相机位姿估计准确度。三维点坐标由基本矩阵分解得到的内参矩阵和外参矩阵转换求出,相机旋转位姿估计的准确与否影响三维点坐标的精确度。

根据上述分析,文中以重建有效三维点数量占比、点云完整度和相机位姿估计准确度为评价标准, 根据影响程度不同设置不同的权重,构建重建精度评价模型,如式(6)所示

   (6)

式中,S a 为重建稠密点云中三维点总数,S e 为重建有效三维点数量,该值由S a 减去噪点数确定,重建产生的噪点应用点云滤波算法[23] 去除,MaxS e 为重建相同物体时不同方法所获取的最大有效三维点数量,I 为点云完整度,定义完成程度为4个级别,由大到小,对应值为1、0.9、0.8、0.7,C 为相机位姿估计准确度,根据相机姿态分4个级别,由大到小,对应值为1、0.9、0.8和0.7,w 1、w 2 和w 3 为对应权重, 根据对后续逆向重建的影响程度,依据层次分析法[24]确定,分别为0.3、0.4和0.3,P 为重建精度, 范围为0~1,数值越大,重建精度越高。

2.2 试验及结果分析

退役零件的形状多种多样,不同形状的零件重建效果不尽相同,退役零件图像集中图像数量不同, 图像分辨率不同,也会影响重建质量。为模拟各种可能的情况,文中选取了形状各不相同的物体,拍摄不同数量的图片构成图像集,各图像集中图像的分辨率各不相同,为了进一步验证文中算法的有效性, 与VisualSFM [25]提供的增量SFM算法、openMVG提供的增量和全局SFM算法进行了比较,选取4个图像集进行试验。

文中基于openMVG开源库进行程序开发,试验环境为处理器Intel Core i5-4200H,3.4GHz,8GB内存, Windows10操作系统, 软件平台为CMVS/PMVS开源库、Geomagic软件、meshlab软件。图像集信息如表1所示。

表1 图像集信息

 

重建后有效三维点组成的稠密点云和相机位姿对比如图3所示。

由图3可见,中部为重建物体的稠密点云,围绕稠密点云呈环形分布的是重建的相机位姿,文中所提自标定全局SFM算法的相机位姿位置估计最为准确,相机位置分布均匀,稠密点云完整度最高。这是由于自标定全局SFM算法使用校准后的相机焦距和三阶径向畸变参数,在求解相机外参矩阵即相机位姿时数值更为精准,点云完整度更高。其次分别为MVG全局算法、MVG增量算法,使用式(2)估计相机焦距, 结果存在一定的偏差。最次为VisualSFM算法,由于使用图像内部的焦距信息作为初始参数,其相机位姿估计有明显的偏差,点云完整度低且存在部分点云漂移。

重建有效稠密点云信息与计算精度如表2所示。

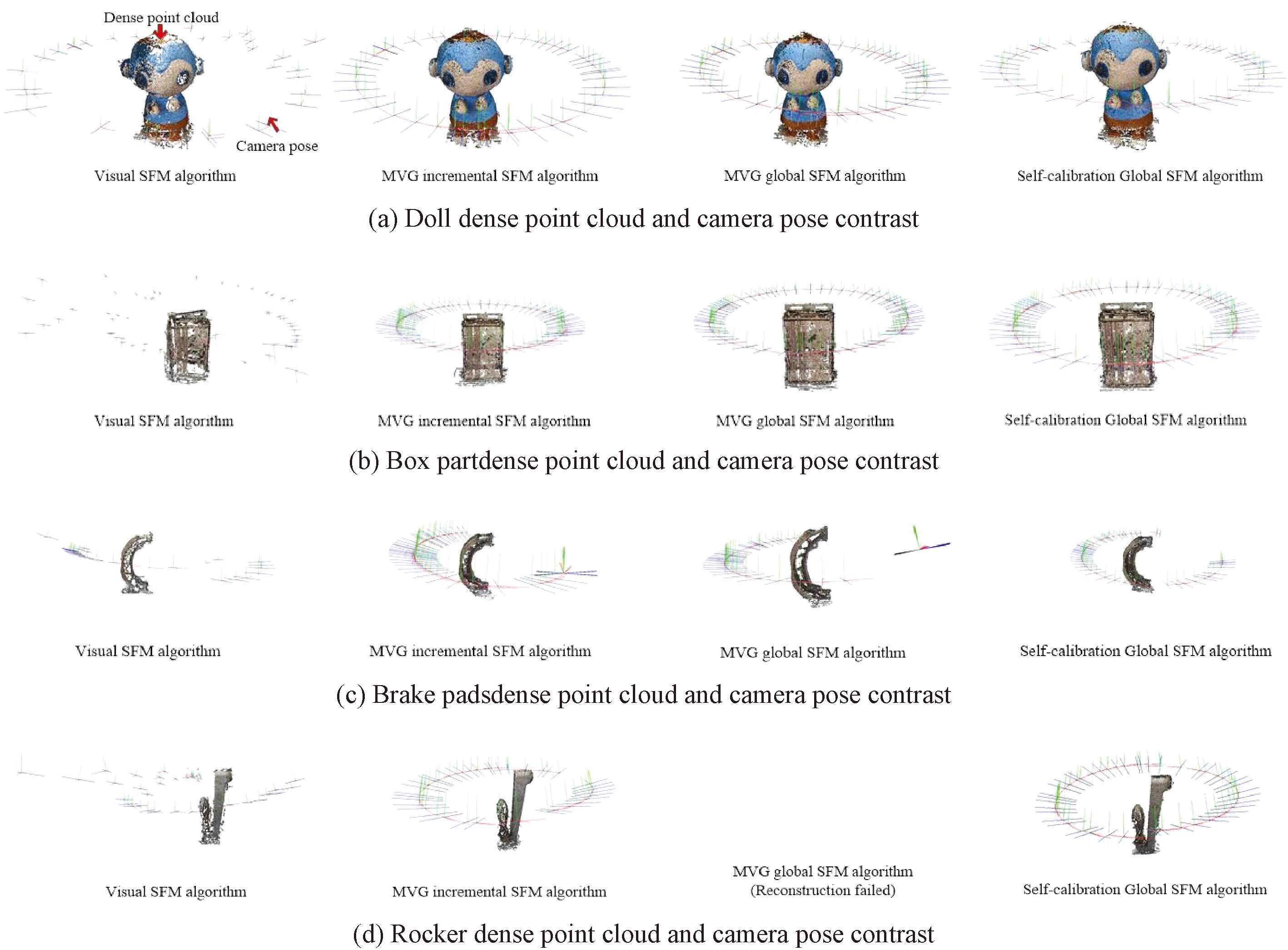
图3 有效稠密点云和相机位姿对比图

表2 点云信息与计算精度表

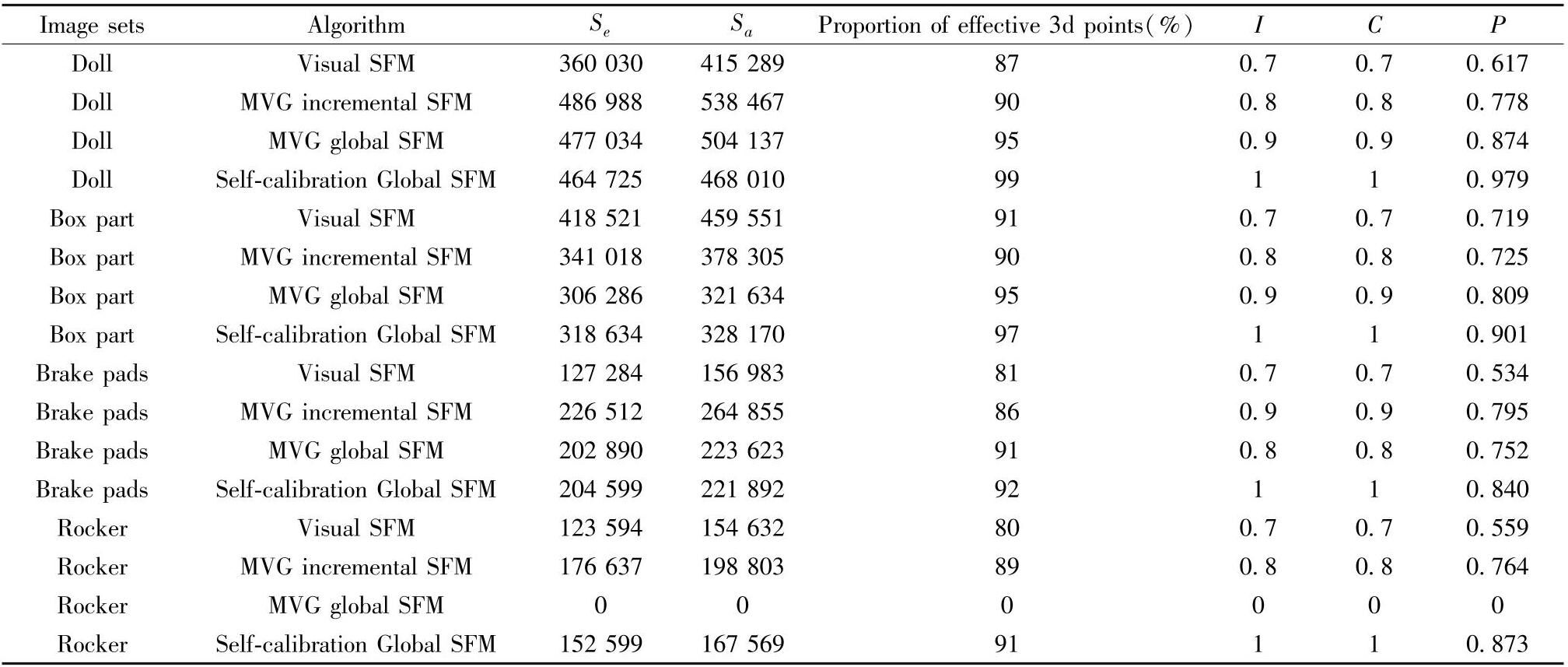
对比表2中三维点参数可知文中算法重建出的稠密三维点云中噪点数量最少,且有效三维点数量占重建三维点总数的比例最高,这是由于校正了相机三阶径向畸变参数,提高了点云中三维点的坐标精度,且全局式算法减少了光束平差的次数,避免了误匹配对被错误的优化到稠密点云中。不同算法重建精度对比如图4所示。

由图4可见,文中算法的重建精度最高,重建精度由高到低分别为玩偶、箱体、摇杆、刹车片。玩偶图像集中图像数量较少,但重建后有效三维点数量和数量占比均较高,原因在于玩偶表面凹凸不平,可类比为磨损不规则且十分严重的零件,这增加了图像间特征点匹配对的数量,降低了误匹配对的数量。其余图像集中图像数量较多,但重建后有效三维点数量和数量占比均较低,原因在于物体表面光滑,基本无磨损且具有一定的金属光泽,这增加了图像间误匹配对的数量,降低了匹配对数量,且刹车片形状不规则,表面存在曲率快速变化的位置,使得一些图像由于特征点过少的原因无法与其它图像相匹配, 进一步降低了重建精度。由于上述问题导致重建精度降低时,可对具有金属光泽的光滑曲面进行着色喷涂,并适当增加曲率快速变化位置的图像数量,以提高重建精度。文中算法重建精度相较MVG全局算法提高10%左右,解决了全局SFM算法重建失败的问题,鲁棒性有所提高。

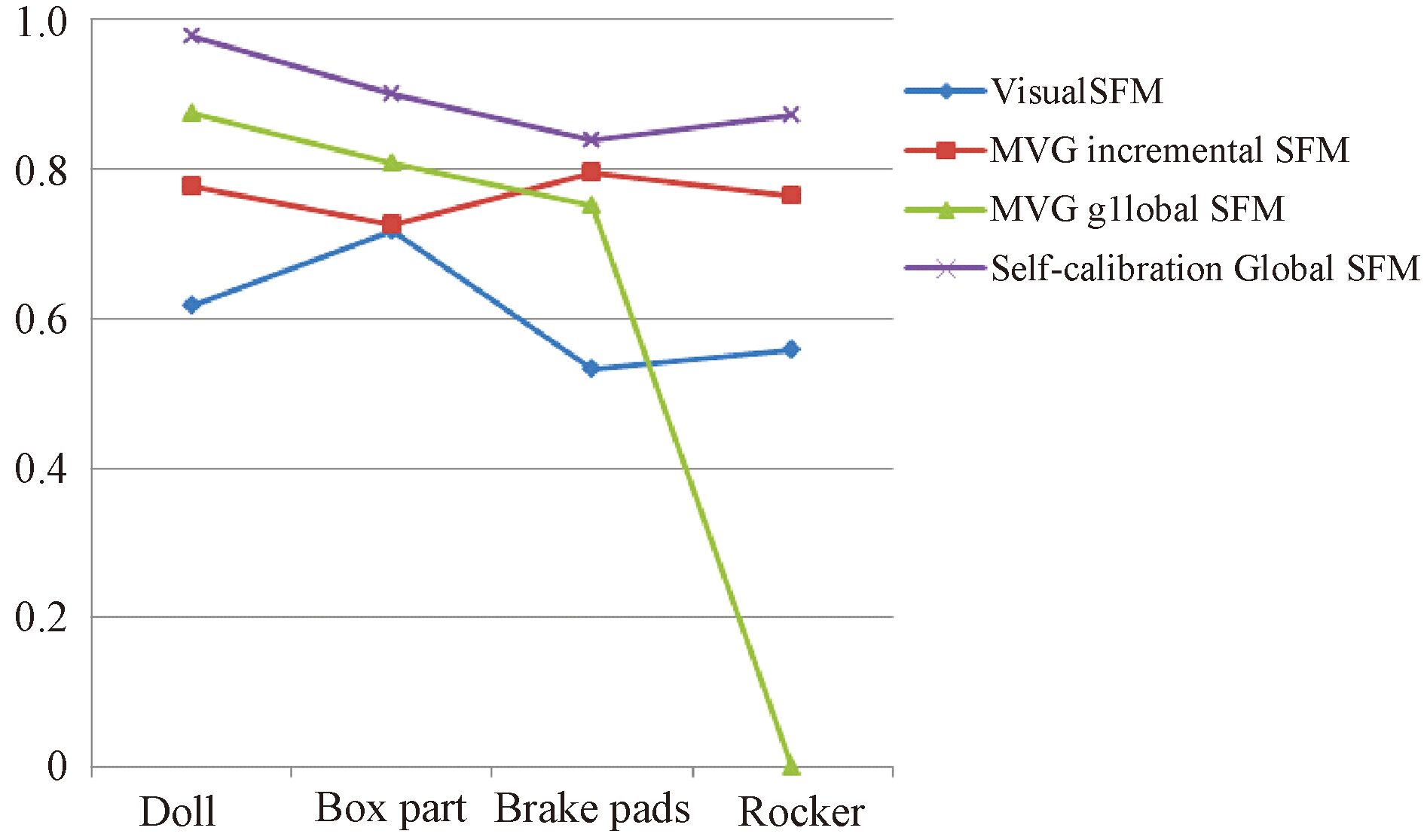
图4 算法精度对比图

自标定全局SFM算法,使用光束平差校准的焦距和径向畸变值作为输入,可以很好的适用于视频中提取出的图像构成的图像集或图片内缺少EXIF信息的情况下的重建,增强了算法的鲁棒性,减少重建后稀疏点云中的噪点数量,提高了精度。

3 表面失效特征表征

表面失效特征表征包括逆向工程重建和失效特征量化两个部分,表面失效特征表征流程如图5所示。

3.1 逆向重建简介

逆向工程重建[26]包括稠密点云处理、多边形处理和曲面处理三部分。稠密点云处理包括稠密点云结构定义,降低点云中的噪点,删除异常点等步骤; 多边形处理主要是对稠密点云进行局部三角化和全局三角化,识别残缺的孔,填充形成多边形模型;曲面处理则是对多边形模型通过三角剖分分解为多个四边形块,经过约束优化使其内角均接近90°且数量尽可能少,并对优化后的四边形进行连接得到非均匀有理B样条曲面[27]构成的三维模型。

3.2 失效特征量化

失效特征量化包括尺寸缩放、质量评估和特征参数对比三部分。

(1) 尺寸缩放。由于图像三维重建过程中对三维点的坐标进行归一化处理,使得逆向工程恢复的三维模型失去了原有的尺寸特征,需要进行尺寸缩放,定义尺寸缩放式(7)为

     (7)

式中,η 为尺寸缩放系数,ΔX b、ΔY b、ΔZ b 为实际两点三维坐标差值,ΔX n、ΔX n、ΔX n 为重建三维模型相同两点三维坐标差值。经过尺寸缩放后即可恢复物体的原有尺寸。

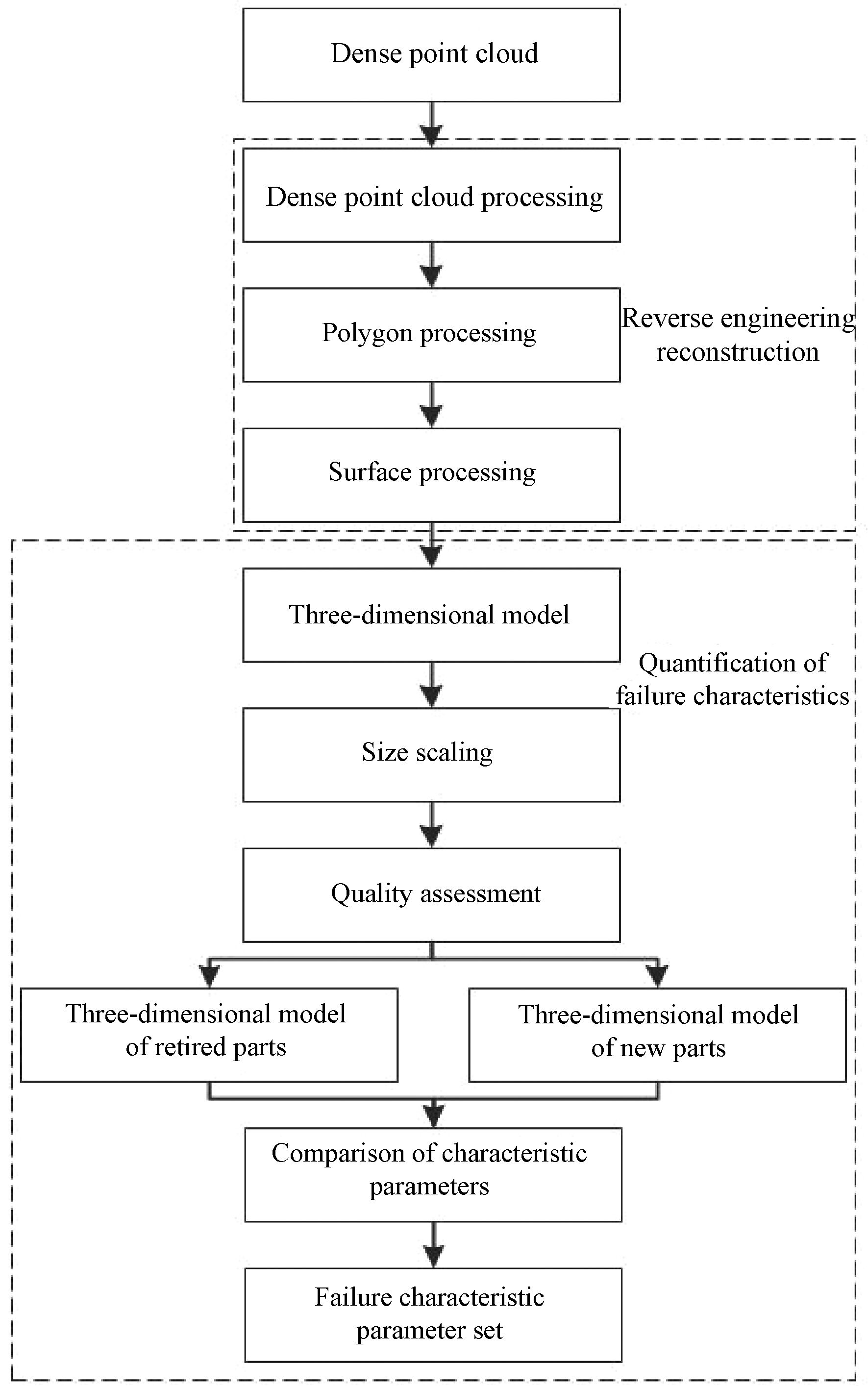
图5 表面失效特征表征流程图

(2) 质量评估。质量评估包括表面积、体积和质量计算,假设重建物的表面为有界曲面,则z=z(x,y),(x,y)∈D xy,其表面积计算公式为

  (8)

体积计算公式为

 (9)

式中,Ω 为重建物体的积分区域。

质量计算公式为

(10)

式中,ρb 为重建物体的密度,I V 为重建物体的体积。通过上式可获得重建物体的表面积、体积、质量特征。

(3) 特征参数对比。参数特征对比旨在比较退役零件特征参数与全新零件特征参数,文中分为两种情况,当已有全新零件的标称三维模型时直接比较特征参数,对比量化退役零件失效特征;缺少全新零件标称三维模型时,应用文中所提方法获取全新零件的标称三维模型,对比量化退役失效特征,失效特征信息集为

式中,S n、I Vn 、M br 分别为全新零件的表面积、体积、质量,S r、I Vr、M br 分别为退役零件的表面积、体积、质量。信息集中包含退役零件的表面积、体积和质量的失效特征信息。

3.3 方法流程

基于图像三维重建的退役零件表面失效特征表征并量化其失效特征包括图像三维重建算法、重建精度评价和表面失效特征量化三个阶段,方法流程如图6所示。

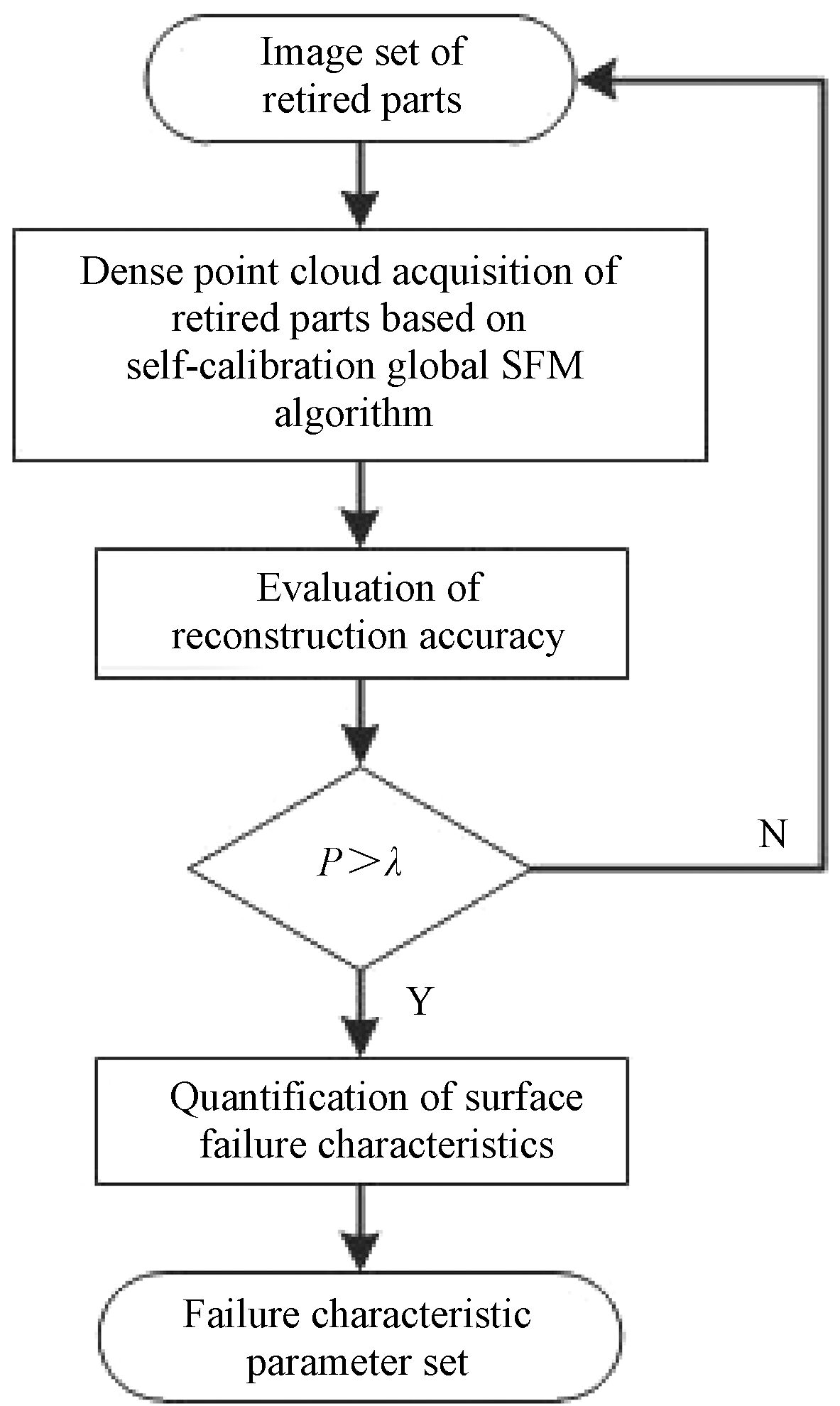
图6 退役零件三维重建失效特征表征方法流程图

步骤如下。

步骤1:构建退役零件图像集。图像集可由相机拍摄获取,也可由视频分解获取。

步骤2:应用自标定全局SFM算法重建退役零件稠密点云。

步骤3:重建精度评价。根据式(6)对退役零件稠密点云进行重建精度评价。

步骤4:重建精度判断。根据重建精度 P 的值判断重建是否成功,当 P 值大于 λ 时认定重建精度符合要求,执行下一步,重建精度小于 λ 时认定重建失败,须重新构建退役零件图像集再次重建。 λ 的值根据客户需求确定,一般大于0.8。

步骤5:表面失效特征量化。对退役零件通过逆向工程重建获取其三维模型,根据式(7) 对三维模型进行尺寸缩放,根据式(8)~(10)求解退役零件失效特征的参数集。

4 案例分析

为了验证文中所提基于图像三维重建的表面失效特征表征方法的有效性,以形状较为复杂,具有复杂的曲面、平面和孔洞的某型退役电梯导靴为例进行验证(图7所示)。由于前文的对比试验已经证明文中所提自标定全局SFM算法在重建精度方面优于其它算法,此处不再进行精度对比试验。

图7 退役和全新导靴实物图

4.1 导靴图像集获取

由于缺乏全新导靴的三维数字化模型,故需要对退役导靴和新导靴分别进行图像三维重建获取其三维模型。

以图7所示的退役和全新导靴为对象,图7a所示退役导靴头部具有一定程度的磨损,使用iPhone11手机拍摄采集了145张退役导靴图片构成退役导靴图像集,每张图片分辨率为4 032×3 024像素, 采集158张全新导靴图片构成全新导靴图像集,每张图片分辨率为4 032×2 724像素。

4.2 导靴三维重建与精度评价

应用自标定全局SFM算法分别对退役导靴图像集和新导靴图像集进行相机自标定,获取相机焦距和三阶径向畸变参数,应用全局SFM算法重建其稀疏点云,应用CMVS/PMVS算法获取退役导靴和新导靴的稠密点云。

将退役导靴和新导靴的稠密点云信息代入点云精度评价式(6) 进行精度评价,其计算结果如表3所示。

表3 导靴点云信息与计算精度表

 

此处,根据客户需求设 λ=0.85,由表3知退役导靴和新导靴的重建精度均大于0.85,满足精度要求,可以进行表面失效特征量化。

4.3 失效特征量化

对退役导靴和全新导靴的稠密点云进行三维重建,经多边形和曲面处理后得到退役导靴和新导靴的三维模型如图8所示。

图8 导靴三维模型

由图8可知,该方法基本重建出了导靴的复杂曲面、平面和孔洞等细节特征。

根据式(7) 对重建后的三维模型进行尺寸缩放,经计算得出尺寸缩放系数为5.6。该导靴材料为灰铸铁,根据式(8)~(10)对其进行质量评估,获取其特征参数和退役导靴失效特征的参数集,具体如表4所示。

表4 失效特征信息对比

 

由表4可知,退役导靴质量为1 715g,新导靴质量为1 856g,对退役导靴和新导靴实物进行质量测量,其质量分别为1 783.8g和1 916.4g,计算得退役导靴重建精度为96.2%,新导靴重建精度为96.8%。

对标退役导靴和新导靴的三维模型,提取出退役导靴磨损部分的三维模型,如图9所示。

图9 导靴磨损部位三维模型图

对其精确形位尺寸进行评估,其质量为138.5g,体积为19.2cm 3,表面积为89.1cm 2,与实际测量的质量132.6g进行比较,获得重建精度为95.7%。

上述计算结果快速精确地量化了导靴的失效特征,可为导靴的可再制造性判断和再制造工艺路线规划提供数据支撑。

5 结论

(1) 提出了自标定全局SFM算法,在构建退役零件图像集的基础上,应用光束平差法进行相机自标定,无需单独标定相机,提高了点云坐标精度和相机位姿估计的准确度,降低了稠密点云中的噪点数量。

(2) 以重建有效三维点数量占比、点云完整度和相机位姿准确度为评价指标,建立退役零件重建精度评价模型,实现了对不同形状物体重建精度的准确评价,为能否进一步表征退役零件失效特征提供理论依据。

(3) 提出了一种基于图像三维重建的退役零件失效特征表征方法,实现了退役零件表面失效特征的高效量化表征,节约成本,获取了退役零件三维模型,可为退役零件再制造评价与修复提供数据支持。

参考文献

[1] 徐滨士.新时代中国特色再制造的创新发展[J].中国表面工程,2018,31(1):1-6.

XU B S.Innovation and development of remanufacturing with Chinese characteristies for a new era [J].China Surface Engineering,2018,31(1):1-6.(in Chinese)

[2] 徐滨士,董世运,史佩京.中国特色的再制造零件质量保证技术体系现状及展望[J].机械工程学报,2013,49(20):84-90.

XU B S,DONG S Y,SHI P J.States and prospects of China characterised quality guarantee technology system for remanufactured parts [J].Journal of Mechanical Engineering,2013,49(20):84-90.(in Chinese)

[3] FU Y D,HU P,TURNER J A,et al.Ultrasonic flaw detection for two-phase Ti-6A1-4V based on secondary scattering[J].NDT and E International,2019,102(MAR):199-206.

[4] WANG W S,QU Z L,ZHENG Z S,et al.Analysis and design of coil-based electromagnetic-induced the rmoacoustic for rail internal-flaw inspectio-n [J].IEEE Transactions on Intelligent Transportati-on Systems,2019,20(7):2691-2702.

[5] KIM K S,KANG S Y,KIM W S,et al.Improvement of radiographic visibility using an image restoration method based on a simple radiographic scatering model for X-ray nondestructive testing[J].N-DT andE International,2018,98:117-122.

[6] 张秀芬,高云飞.退役机械零部件多维递阶再制造性评价方法[J].浙江大学学报,2020,54(5):954-962.

ZHANG X F,GAO Y F.Multi-dimensional hierar-chical remanufacturability evaluation method for e-nd-of-life mechanical parts [J].Journal of Zhejiang University,2020,54(5):954-962.(in Chinese)

[7] ZHANG X,CUI W,LI W,et al.A hybrid process integrating reverse engineering,prerepair processing,additive manufacturing,and material testing for component remanufacturing[J].Materials,2019,12(12):1961.

[8] 毕天腾,刘越,翁冬冬,等.基于监督学习的单幅图像深度估计综述[J].计算机辅助设计与图形学学报,2018,30(8):1383-1393.

BI T T,LIU Y,WENG D D,et al.Survey on supervised learning based depth estimation from a single image[J].Journal of Computer-Aided Design and Computer Graphics,2018,30(8):1383-1393.(in Chinese)

[9] XU J,WANG K,GAO M,et al.Biomechanical performance design of joint prosthesis for medical rehabilitation via generative structure optimization [J].Computer Methods in Biomechanics and Biomedical Engineering,2020,23(15):1-17.

[10] JEON H G,SURH J,IM S,et al.Ring differencefilter for fast and noise robust depth from focus [J].IEEE Transactions on Image Processing,2019,29:1045-1060.

[11] 程亚楠,刘晓东,张东升,等.利用测深侧扫数据和明暗恢复形状方法实现地形修正[J].仪器仪表学报,2019,40(7):159-168.

CHENG Y N,LIU X D,ZHANG D S,et al.R-ealization of terrain correction utilizing bathymetric sidescan data and shape from shading methods [J].Chinese Journal of Scientific Instrument,2019,40(7):159-168.(in Chinese)

[12] 张洪鑫,王明珠,仇浩然,等.基于单目图像序列的铸件三维重建方法[J].中国机械工程,2018,29(23):2799-2803.

ZHANG H X,WANG M Z,QIU H R,et al.3Dreconstruction method of castings based on monocular image sequences [J].China Mechanical Engineering,2018,29(23):2799-2803.(in Chinese)

[13] YU Y J,WANG G F,ZHAO J.FI-SIFT algorithm for exposing image copy-move forgery with reflection attacks[J].International Journal of Network Security,2020,22(2):183-190.

[14] HASSANIN A A I M,El-SAMIE F E A,BANBY G M E.A real-time approach for automatic defect detection from PCBs based on SURF features and morphological operations [J].Multimedia Tools and Applications,2019,78(24):34437-34457.

[15] MUKHERJEE P,LALL B.Saliency and KAZE features assisted object segmentation [J].Image and Vision Computing,2017,61:82-97.

[16] WANG N N,GAO X B,LI J.Random samplingfor fast face sketch synthesis[J].Pattern Recognition,2018,76:215-227.

[17] 陈辉,杨剑,黄晓铭,等.基于多视图立体视觉的沙堆三维尺寸测量研究[J].计量学报,2019,40(3):403-408.

CHEN H,YANG J,HHUANG X M,et al.Research on 3D measurement of sand pile based on multi view stereo vision[J].Acta Metrologica Sinica,2019,40(3):403-408.(in Chinese)

[18] 董建伟,李海滨,孔德明,等.基于多视图立体视觉的煤场三维建模方法研究 [J].燕山大学学报,2016,40(2):136-141.

DONG J W,LI H B,KONG D M,et al.Research on 3D modeling of coal field based on multi-view stereo vision method [J].Journal of Yanshan University,2016,40(2):136-141.(in Chinese)

[19] 鲁晨曦.基于图像的全局SFM三维模型重建方法研究与实现[D].成都:电子科技大学,2017.

LU C X.Image-based three-dimensional model re-constructionUsing global structure from motion [ D].Chengdu:University of Electronic Science and Technology of China,2017.(in Chinese)

[20] MOISAN L,MOULON P.Automatic homographicregistration of a pair of images,with a contrario elimination of outliers[J].Image Processing on Line,2012(2):56-73.

[21] ZHANG Z Y.Flexible camera calibration by vie-wing a plane from unknown orientations [ C ]//Seventh IEEE International Conference on Computer Vision.IEEE,1999.

[22] MOULON P,MONASSE P,MARLET R.Adapti-ve structure from motion with a contrario model estimation [ C]//Computer Vision-ACCV 2012.

ACCV,2012.

[23] 冯发杰,丁亚洲,吏军平,等.使用显著性划分的机载激光雷达点云滤波[J].红外与激光工程,2020,49(8):26-34.

FENG F J,DING Y Z,SHI L J,et al.AirborneLiDAR point cloud filtering using saliency divisi-on [J].Infrared and Laser Engineering,2020,49(8):26-34.(in Chinese)

[24] 任仲贺,武美萍,唐又红,等.机械设备零部件再制造评价点阵图模型及应用 [J].中国表面工程,2018,31(6):143-152.

REN Z H,WU M P,TANG Y H,et al.Dot matrix model of remanufacturing evaluation for mechanical equipment parts and its application [J].China Surface Engineering,2018,31(6):143-152.(in Chinese)

[25] WU C C.Towards linear-time incremental structure from motion [C]//3DV-Conference,2013 Intern-ational Conference on IEEE Computer Society,2013.

[26] FLETCHER Y G,GLOTH T,EDELSBRUNNER H,et al.Methods,apparatus and computer program products that reconstruct surfaces from data po-int sets[P].US:US7023432,2006-04-04.

[27] 黄海博,孙文磊,张冠,等.基于NURBS曲面的汽轮机叶片激光熔覆再制造路径规划[J].中国表面工程,2018,31(5):175-183.

 

HUANG H B,SUN W L,ZHANG G,et al.Pathtrajectory of laser cladding remanufacturing for turbine blade based on NURBS surface [J].China Surface Engineering,2018,31(5):175-183(in Chinese).