关于热疲劳、热分析、热疲劳可靠性分析的专业技术知识介绍
2020-04-03 14:52:39
作者:本网整理 来源:可靠性知识
分享至:
热疲劳
金属材料由于温度梯度循环引起的热应力循环(或热应变循环),而产生的疲劳破坏现象,称为热疲劳。金属零件在高温条件下工作时,其环境温度并不恒定,而有时是急剧反复变化的。由此造成的膨胀和收缩若受到约束时,在零件内部就会产生热应力(又称温差应力)。温度反复变化,热应力也随着反复变化,从而使材料受到疲劳损伤。塑性材料抗热应变的能力较强,故不易发生热疲劳。相反,脆性材料抗热应变的能力差,热应力容易达到材料的断裂应力故易受热冲击而破坏。(2)裂纹走向可以是沿晶型的,也可以是穿晶型的;一般裂纹端部较尖锐,裂纹内有或充满氧化物。(4)裂纹源于表面,裂纹扩展深度与应力、时间及温差变化相对应。(1)环境的温度梯度及变化频率越大越易产生热疲劳。(4)晶界分布的第二相质点对热疲劳的产生,具有促进作用。(6)零件的几何结构对金属的膨胀和收缩的约束作用大,易出现热疲劳。
热分析,又称热模拟,是利用数学手段,在电子产品的设计阶段获得温度分布的方法,它可以使电子产品设计人员和可靠性设计人员在设计初期就能发现产品的热缺陷,从而改进其设计,为提高产品设计的合理性及可靠性提供有力保障。
热分析需建立电子产品温度场和流场的数学模型,并对其求解,由于求解的复杂性,热分析大都采用软件来完成。国外有很多公司已经开发了电产品热分析软件,并且大多数已经商品化。应用软件进行热分析的基本步骤为:
(a)根据或设计要求建立热分析模型,确定边界条件;(c)后处理,以报表、图形或动画的形式观察温度场。热分析软件虽能较准确的获得温度场的分布,但在应用过程中可能存在建模不合理,输入参数的不准确等原因而导致热分析误差较大,不能满足工程要求。
热分析模型建立的不准确,会导致较大的热分析误差,不能满足工程要求。对于准确的模型,如果过于复杂,又会占用大量的计算机资源和计算时间;如果过于简单,则计算结果可能会忽略大量的细节,而达不到分析的目的。建模的策略是由重要到次要,由简单到复杂。即从最重要的入手,比如确定整体布局,对壁、外壳、开孔、功耗、电路板等进行建模;在这基础上,再加入其它较重要的影响因素,比如器件的布局与建模,外壳与外界的热交换等等;对重点分析部位进行详细建模(例如对关键发热元器件进行三维详细建模);对于次要因素,进行粗略建模,甚至忽略掉(例如对于发热很小或不发热的元器件)。
输入参数的准确与否,极大地影响着热分析结果。输入参数主要包括材料的热传导率、元器件的热功耗、初始条件等等,其中传导率等可通过查工程热设计手册、实验或反复修正来得到,初始条件可通过测量得到,热功耗可以通过查产品手册或电路仿真的方法得到。
划分网格的多少在一定程度上影响着热分析的结果,通常网格划分的越多,则计算精度越高,但网格过多计算时间将过长,而精度得不到明显的提高。因此应灵活运用网格划分技术,在重要部位(如温度梯度高的位置,芯片位置等)进行局部加密,在不规则形状处采用非结构化网格。作为一个示例,采用某热分析软件对一个板级电路进行热分析。

图1 某印刷电路板的热分析模型
在电路板的属性菜单设置电路板的几何尺寸、层的厚度和电路板中金属部分的传导率(例如铜的传导率为388W/m.K)等参数。 如是稳态热分析,初始条件可设为0,如不是稳态分析,可设置开始时刻的温度值;设置每个器件的功耗;器件的热传导率,对于详细建模的器件还应分别输入其金属部分的热传导率和非金属部分的热传导率;电路板的工作环境条件,包括电路板在机箱中的位置、空气流动情况、邻近电路板或机箱壁的热效应等。 进入网格划分菜单,选择相邻网格间的宽度和高度,计算机自动划分网格。 进入后处理菜单,可选择多种查看结果的方法。例如温度分布图,温度梯度分布图,等温图等,图2为该电路板的温度分布图,以不同的颜色代表不同的温度值。
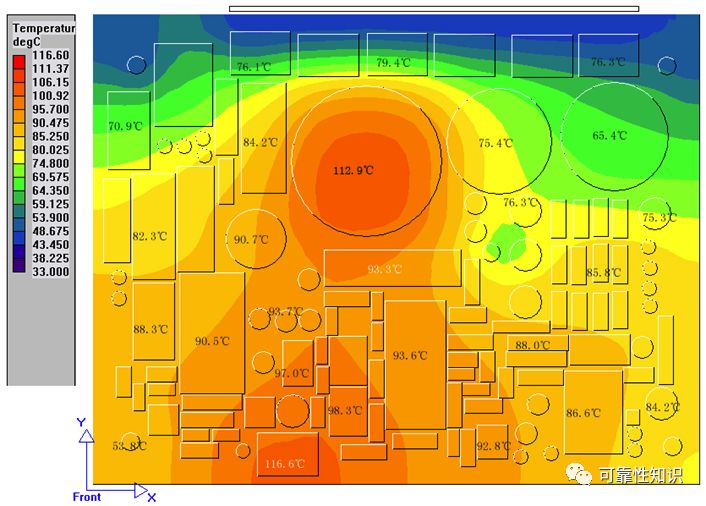
图2 某印刷电路板的温度分布图
91质量网开发了专业的分布式多学科协同可靠性仿真软件(了解更多内容,请本公众号回复“分布式仿真”),在热疲劳可靠性仿真分析方面,已在核工业、航空、风电、兵器等领域得到广泛应用。
热疲劳可靠性分析是热疲劳分析与可靠性分析的一体化,在分析时,很多情况下难以直接建立应力、应变、位移等与载荷、材料、结构尺寸的关系,往往需要借助热分析CAE工具进行分析,这种情况下反映为功能函数与基本随机变量的关系是隐式的。
从可靠度计算的角度分析,模拟法和响应面法一般只需要获得功能函数在给定样本点的值,这些值可以借助热分析CAE工具分析获得,再对结果进行统计来计算可靠度;一次可靠度法不仅需要计算功能函数的值,还需要获得功能函数关于随机向量的梯度。
利用热分析CAE工具进行可靠性仿真计算,必须解决以下2个问题:
(1)可靠度计算程序对热分析CAE软件的封装和调用,以实现功能函数值的计算;
(2)梯度的计算,这可以在获得功能函数值的基础上采用有限差分法计算。
因此关键是实现利用热分析CAE工具实现功能函数值的计算。
有两种实现可靠性仿真计算的思路:抽样仿真和迭代仿真,如图3所示。
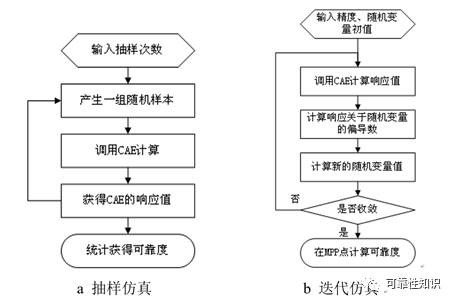
图3 可靠性仿真的流程
免责声明:本网站所转载的文字、图片与视频资料版权归原创作者所有,如果涉及侵权,请第一时间联系本网删除。









